
【题目】假设要考察某公司生产的流感疫苗的剂量是否达标,现从500支疫苗中抽取50支进行检验,利用随机数表法抽取样本时,先将500支疫苗按![]() 进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号________.(下面摘取了随机数表第7行至第9行)
进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号________.(下面摘取了随机数表第7行至第9行)
第7行:84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50
25 83 92 12 06 76
第8行:63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58
07 44 39 52 38 79
第9行:33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13
42 99 66 02 79 54
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】随着互联网的快速发展,基于互联网的共享单车应运而生,某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
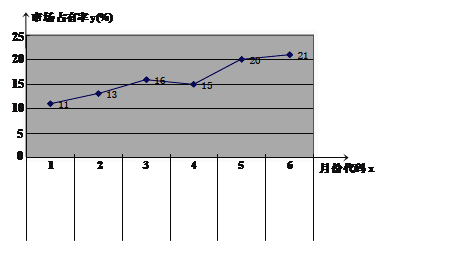
(1)由折线图可以看出,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并
的线性回归方程,并
预测![]() 公司2017年4月的市场占有率;
公司2017年4月的市场占有率;
(2)为进一步扩大市场,公司拟再采购一批单车,现有采购成本分别为![]() 元/辆和1200元/辆的
元/辆和1200元/辆的![]() 、
、![]() 两款车型可供选择,按规定每辆单车最
两款车型可供选择,按规定每辆单车最
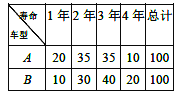
多使用4年,但由于多种原因(如骑行频率等)会导致单车使用寿命各不相同,考虑到公司运营的经济效益,该公司决定先对这两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命的频数表如右表:经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率,如果你是![]() 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考公式:回归直线方程为![]() ,其中
,其中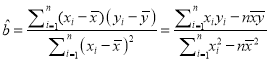 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() .
. ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 上任意一点.
上任意一点.
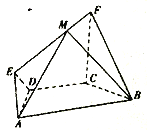
(1)求证: ![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动(包括两端点),若平面
上运动(包括两端点),若平面![]() 与平面
与平面![]() 所成的锐二面角为60°,试确定点
所成的锐二面角为60°,试确定点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为![]() ,则称该数为“完美四位数”,如数字“
,则称该数为“完美四位数”,如数字“![]() ”.试问用数字
”.试问用数字![]() 组成的无重复数字且大于
组成的无重复数字且大于![]() 的“完美四位数”有( )个
的“完美四位数”有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为![]() (
(![]() ).
).
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l与x正半轴、射线![]() (
(![]() )分别交于P,Q两点,当a为何值时,
)分别交于P,Q两点,当a为何值时,![]() 的面积最小?
的面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任一点,若直线
上任一点,若直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() .
.
(1)求椭圆的方程;
(2)若![]() 交直线
交直线![]() 于
于![]() 两点,过左焦点
两点,过左焦点![]() 作以
作以![]() 为直径的圆的切线.问切线长是否为定值,若是,请求出定值;若不是,请说明理由.
为直径的圆的切线.问切线长是否为定值,若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取
的参赛者中,利用分层抽样的方法随机抽取![]() 人参加学校座谈交流,那么从得分在区间
人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的![]() 人中,选出
人中,选出![]() 人参加全市座谈交流,设
人参加全市座谈交流,设![]() 表示得分在区间
表示得分在区间![]() 中参加全市座谈交流的人数,求
中参加全市座谈交流的人数,求![]() 的分布列及数学期望E(X).
的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元。
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得下表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com