【题目】请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得
四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE=FB=xcm2
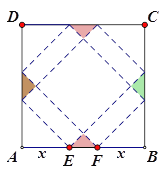
（1）若广告商要求包装盒侧面积S（cm
）最大，试问x应取何值？
（2）若广告商要求包装盒容积V（cm
）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值。
科目：高中数学 来源： 题型：
【题目】如图，在底面是菱形的四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=60°，PA=AB=2，点E，F分别为BC，PD的中点，设直线PC与平面AEF交于点Q．
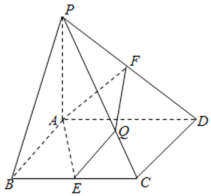
（1）已知平面PAB∩平面PCD=l，求证：AB∥l．
（2）求直线AQ与平面PCD所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）是定义域为R的偶函数，且f（x+3）=f（x-1），若当x∈[-2，0]时，f（x）=2-x，记
，
，c=f（32），则a，b，c的大小关系为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知椭圆C：
的左、右顶点为A，B，右焦点为F.过点A且斜率为k（
）的直线交椭圆C于另一点P.
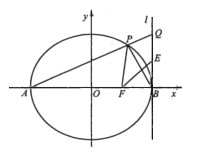
（1）求椭圆C的离心率；
（2）若
，求
的值；
（3）设直线l:
，延长AP交直线l于点Q，线段BQ的中点为E，求证：点B关于直线EF的对称点在直线PF上.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成，
米，如图所示．小球从A点出发以5 V的速度沿半圆O轨道滚到某点E处后，经弹射器以6 V的速度沿与点E切线垂直的方向弹射到落袋区BC内，落点记为F．设
弧度，小球从A到F所需时间为T．
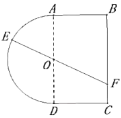
（1）试将T表示为
的函数
，并写出定义域；
（2）当满足什么条件时，时间T最短．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某文体局为了解“跑团”每月跑步的平均里程，收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程（单位：公里）的数据，绘制了下面的折线图.根据折线图，下列结论正确的是（ ）
A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月，波动性更小，变化比较平稳
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
（
）的离心率为
，且过点
，椭圆的右顶点为
.
（Ⅰ）求椭圆的的标准方程；
（Ⅱ）已知过点
的直线交椭圆于
，
两点，且线段
的中点为
，求直线
的斜率的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
（
（1）当a＝0时，求f（x）的极值；
（2）当a＞0时，讨论f（x）的单调性；
（3）若对任意的a∈（2, 3），x1, x2∈[1, 3]，恒有（m－ln3）a－2ln3＞|f（x1）－f（x2）|成立，求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
