
【题目】已知函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)用![]() 表示
表示![]() 中较大者,记函数
中较大者,记函数![]() .若函数
.若函数![]() 在
在![]() 上恰有2个零点,求实数a的取值范围.
上恰有2个零点,求实数a的取值范围.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题可得![]() ,结合
,结合![]() 的范围判断
的范围判断![]() 的正负,即可求解;
的正负,即可求解;
(2)结合导数及函数的零点的判定定理,分类讨论进行求解
(1)![]() ,
,
①当![]() 时,
时,![]() ,
,
∴函数![]() 在
在![]() 内单调递增;
内单调递增;
②当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,则
,则![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,则
,则![]() 单调递减,
单调递减,
∴函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]()
(2)(Ⅰ)当![]() 时,
时,![]() 所以
所以![]() 在
在![]() 上无零点;
上无零点;
(Ⅱ)当![]() 时,
时,![]() ,
,
①若![]() ,即
,即![]() ,则
,则![]() 是
是![]() 的一个零点;
的一个零点;
②若![]() ,即
,即![]() ,则
,则![]() 不是
不是![]() 的零点
的零点
(Ⅲ)当![]() 时,
时,![]() ,所以此时只需考虑函数
,所以此时只需考虑函数![]() 在
在![]() 上零点的情况,因为
上零点的情况,因为![]() ,所以
,所以
①当![]() 时,
时,![]() 在
在![]() 上单调递增。又
上单调递增。又![]() ,所以
,所以
(ⅰ)当![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
(ⅱ)当![]() 时,
时,![]() ,又
,又![]()
![]() ,所以此时
,所以此时![]() 在
在![]() 上恰有一个零点;
上恰有一个零点;
②当![]() 时,令
时,令![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因为![]() ,
,![]() ,所以此时
,所以此时![]() 在
在![]() 上恰有一个零点,
上恰有一个零点,
综上,![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围;
的取值范围;
(3)设![]() 是函数
是函数![]() 的导函数,
的导函数,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 的零点为
的零点为![]() ,则点
,则点![]() 恰好就是该函数
恰好就是该函数![]() 的对称中心.试求
的对称中心.试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知BD为圆锥AO底面的直径,若![]() ,C是圆锥底面所在平面内一点,
,C是圆锥底面所在平面内一点,![]() ,且AC与圆锥底面所成角的正弦值为
,且AC与圆锥底面所成角的正弦值为![]() .
.
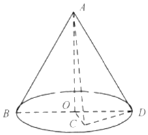
(1)求证:平面![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,动点P与定点![]() 的距离和它到定直线
的距离和它到定直线![]() 的距离之比是
的距离之比是![]() ,设动点P的轨迹为E.
,设动点P的轨迹为E.
(1)求动点P的轨迹E的方程;
(2)设过F的直线交轨迹E的弦为AB,过原点的直线交轨迹E的弦为CD,若![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有![]() 人参加,现将所有参加者按年龄情况分为
人参加,现将所有参加者按年龄情况分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等七组,其频率分布直方图如图所示,已知
等七组,其频率分布直方图如图所示,已知![]() 这组的参加者是6人.
这组的参加者是6人.
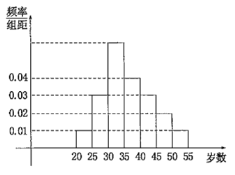
(1)根据此频率分布直方图求![]() ;
;
(2)已知![]() ,
,![]() 这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率.
这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年由于猪肉涨价太多,更多市民选择购买鸡肉、鸭肉、鱼肉等其它肉类.某天在市场中随机抽出100名市民调查,其中不买猪肉的人有30位,买了肉的人有90位,买猪肉且买其它肉的人共30位,则这一天该市只买猪肉的人数与全市人数的比值的估计值为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列命题:
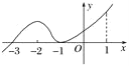
①-3是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在区间(-3,1)上单调递增;
④y=f(x)在x=0处切线的斜率小于零.
以上正确命题的序号是( )
A. ①②B. ③④C. ①③D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com