
【题目】已知椭圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,
,![]() 上的点
上的点![]() 与
与![]() 的两个焦点所构成的三角形的周长为
的两个焦点所构成的三角形的周长为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() ∥
∥![]() .判断
.判断![]() 是否为定值,若是求出该值;若不是请说明理由.
是否为定值,若是求出该值;若不是请说明理由.
【答案】(1)![]() (2)是定值,
(2)是定值,![]() 为定值2.
为定值2.
【解析】
(1)先求出抛物线![]() 的焦点
的焦点![]() 的坐标,再由
的坐标,再由![]() 经过点
经过点![]() 得出
得出![]() 的值,最后利用椭圆的定义以及题中条件求出
的值,最后利用椭圆的定义以及题中条件求出![]() ,从而得解;
,从而得解;
(2)先设出直线![]() 的方程,求出点
的方程,求出点![]() 的坐标,可得
的坐标,可得![]() 的值,再把
的值,再把![]() 的方程与
的方程与![]() 的方程联立,求出点
的方程联立,求出点![]() 的坐标,从而得
的坐标,从而得![]() 的值,根据已知求出
的值,根据已知求出![]() ,根据椭圆的对称性,求出
,根据椭圆的对称性,求出![]() ,即可判断
,即可判断![]() 是否为定值.
是否为定值.
(1)因为抛物线![]() 的焦点
的焦点![]() ,所以
,所以![]() ,
,
因为![]() 上的点
上的点![]() 与
与![]() 的两个焦点所构成的三角形的周长为
的两个焦点所构成的三角形的周长为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的方程为
的方程为![]() .
.
(2)由题意可知直线![]() 的斜率存在且不为0,设直线
的斜率存在且不为0,设直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() ,
,
由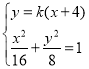 ,得
,得![]() ,解得
,解得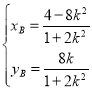 ,
,
即 , 所以
, 所以![]() ,
,
因为![]() ∥
∥![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
由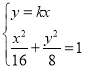 ,得
,得![]() ,解得
,解得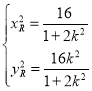 ,
,
所以![]() ,
,
根据椭圆的对称性,知![]() ,即
,即![]() ,
,
所以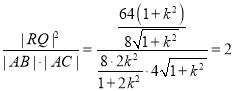 ,
,
故![]() 为定值,该定值为2.
为定值,该定值为2.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,右准线为
,右准线为![]() .过点
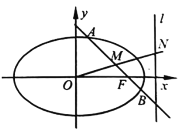
.过点![]() 作与坐标轴都不垂直的直线与椭圆
作与坐标轴都不垂直的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且直线
为坐标原点,且直线![]() 与右准线
与右准线![]() 交于点
交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得
,使得![]() 恒成立?若存在,求实数
恒成立?若存在,求实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有一块半径为R的扇形AOB公园,其中O为扇形所在圆的圆心,AOB=![]() ,OA,OB,
,OA,OB,![]() 为公园原有道路.为满足市民观赏和健身的需要,市政部门拟在
为公园原有道路.为满足市民观赏和健身的需要,市政部门拟在![]() 上选取一点M,新建道路OM及与OA平行的道路MN(点N在线段OB上),设AOM=
上选取一点M,新建道路OM及与OA平行的道路MN(点N在线段OB上),设AOM=![]() .
.

(1)如何设计,才能使市民从点O出发沿道路OM,MN行走至点N所经过的路径最长?请说明理由;
(2)如何设计,才能使市民从点A出发沿道路![]() ,MN行走至点N所经过的路径最长?请说明理由.
,MN行走至点N所经过的路径最长?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的奇函数,其中
上的奇函数,其中![]() ,则下 列关于函数
,则下 列关于函数![]() 的描述中,其中正确的是( )
的描述中,其中正确的是( )
①将函数![]() 的图象向右平移
的图象向右平移![]() 个单位可以得到函数
个单位可以得到函数![]() 的图象;
的图象;
②函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() ;
;
③当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
④函数![]() 在
在![]() 上单调递增.
上单调递增.
A.①③B.③④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某原料在市场上从2013年至2019年这7年中每年的平均价格(单位:千元/吨)数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
平均价格 (单位:千元/吨) |
|
|
|
|
|
|
|
(![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程(系数精确到
为预报变量的线性回归方程(系数精确到![]() );
);
(2)以(1)的结论为依据,预测2032年该原料价格.预估该原料价格在哪一年突破1万元/吨?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: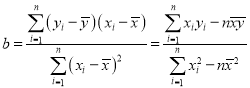 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,离心率为
,离心率为![]() , 在
, 在![]() 轴负半轴上有一点
轴负半轴上有一点![]() ,且
,且![]()
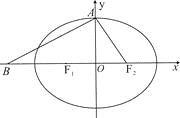
(1)若过![]() 三点的圆 恰好与直线
三点的圆 恰好与直线![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(2)在(1)的条件下,过右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出![]() 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线
,准线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.
![]() 若
若![]() ,
,![]() ,求直线
,求直线![]() 的方程;
的方程;
![]() 若
若![]() ,点
,点![]() 为准线
为准线![]() 上任意一点,求证:直线
上任意一点,求证:直线![]() ,
,![]() ,
,![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出![]() 、
、![]() 两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于
两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于![]() 时为废品,指标值在
时为废品,指标值在![]() 为一等品,大于
为一等品,大于![]() 为特等品.现把测量数据整理如下,其中
为特等品.现把测量数据整理如下,其中![]() 配方废品有
配方废品有![]() 件.
件.
![]() 配方的频数分布表
配方的频数分布表
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)求![]() ,
,![]() 的值;
的值;
(2)试确定![]() 配方和
配方和![]() 配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com