
| A. | b≥0 | B. | b<0 | C. | 3a+c≤0 | D. | 3a-c<0 |
分析 分别判断出a>0,c<0,根据b2-4a(a+c)=b(b+4a)=b(3a-c)≥0,求出3a-c>0,从而判断出b≥0.
解答 解:∵函数f(x)=ax2+bx+c(a>b>c),满足f(1)=0,
∴a+b+c=0.
若a≤0,∵a>b>c∴b<0,c<0,
则有a+b+c<0,这与a+b+c=0矛盾,∴a>0成立.
若c≥0,则有b>0,a>0,此时a+b+c>0,这与a+b+c=0矛盾,
∴c<0成立.
∵a2+[f(m1)+f(m2)]•a+f(m1)•f(m2)=0
∴[a+f(m1)]•[a+f(m2)]=0,∴m1,m2是方程f(x)=-a的两根
∴△=b2-4a(a+c)=b(b+4a)=b(3a-c)≥0
而a>0,c<0∴3a-c>0,
∴b≥0.
故选:A.
点评 本题考查了二次函数的性质,考查转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
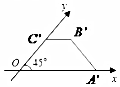
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
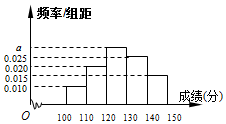 某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有300人.
某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有300人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
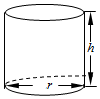 某工厂打算建造如图所示的圆柱形容器(不计厚度,长度单位:米),按照设计要求,该容器的底面半径为r,高为h,体积为16π立方米,且h≥2r.已知圆柱的侧面部分每平方米建造费用为3千元,圆柱的上、下底面部分每平方米建造费用为a千元,假设该容器的建造费用仅与其表面积有关,该容器的建造总费用为y千元.
某工厂打算建造如图所示的圆柱形容器(不计厚度,长度单位:米),按照设计要求,该容器的底面半径为r,高为h,体积为16π立方米,且h≥2r.已知圆柱的侧面部分每平方米建造费用为3千元,圆柱的上、下底面部分每平方米建造费用为a千元,假设该容器的建造费用仅与其表面积有关,该容器的建造总费用为y千元.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com