练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的离心率为，且经过点P，过它的左、右焦点分别作直线l1和12.l1交椭圆于A.两点，l2交椭圆于C,D两点， 且

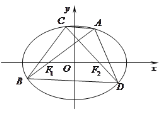
    (1)求椭圆的标准方程.

    (2)求四边形ACBD的面积S的取值范围.

    【答案】（1）；（2）

    【解析】

    （1）由题得关于的方程组，解方程组即得椭圆的标准方程;（2）当与中有一条直线的斜率不存在，则另一条直线的斜率为0，求出此时四边形的面积；若与的斜率都存在，设的斜率为，则的斜率为．求出，再利用基本不等式求S的取值范围.

    （1）由得，所以，

    将点P的坐标代入椭圆方程得，

    故所求椭圆方程为.

    （2）当与中有一条直线的斜率不存在，则另一条直线的斜率为0，

    此时四边形的面积为，

    若与的斜率都存在，设的斜率为，则的斜率为．

    直线的方程为，设，，联立，

    消去整理得，

    ，，

    ，

    同理得，

    所以，

    令，

    ，

    (当且仅当t=1时取到等号)

    综上可知，四边形面积的.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每种单价（元）试销l天，得到如表单价（元）与销量（册）数据：

    单价（元）

    18

    19

    20

    21

    22

    销量（册）

    61

    56

    50

    48

    45

    （l）根据表中数据，请建立关于的回归直线方程：

    （2）预计今后的销售中，销量（册）与单价（元）服从（l）中的回归方程，已知每册书的成本是12元，书店为了获得最大利润，该册书的单价应定为多少元？

    附：，，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体ABCD－A′B′C′D′的棱长为a，连接A′C′，A′D，A′B，BD，BC′，C′D，得到一个三棱锥.求：

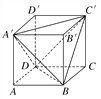
    (1)三棱锥A′－BC′D的表面积与正方体表面积的比值；

    (2)三棱锥A′－BC′D的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝x2+1，g（x）＝4x+1，的定义域都是集合A，函数f（x）和g（x）的值域分别为S和T，

    （1）若A＝[1，2]，求S∩T

    （2）若A＝[0，m]且S＝T，求实数m的值

    （3）若对于集合A的任意一个数x的值都有f（x）＝g（x），求集合A．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，；

    （1）写出函数的最小正周期；

    （2）请在下面给定的坐标系上用“五点法”画出函数在区间的简图；

    （3）指出该函数的图象可由的图象经过怎样的平移和伸缩变换得到？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有个人聚会，已知：

    （1）每个人至少同其中个人互相认识；

    （2）对于其中任意个人，或者其中有2人相识，或者余下的人中有2人相识，证明：这个人中必有3人两两相识.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设双曲线的两支为(如图)，正三角形PQR的三顶点位于此双曲线上。

    （1）求证：P、Q、R不能都在双曲线的同一支上；

    （2）设P(-1，-1)在上，Q、R在上。求顶点Q、R的坐标。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)若函数的图象与轴无交点，求的取值范围；

    (2)若函数在上存在零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数恰有一个零点，求实数的取值范围；

    （2）设关于的方程的两个不等实根，求证：（其中为自然对数的底数）.

    查看答案和解析>>

    同步练习册答案