
【题目】已知正实数x,y满足 ![]() +2y﹣2=lnx+lny,则xy= .
+2y﹣2=lnx+lny,则xy= .
【答案】![]()
【解析】解:令f(x)= ![]() ﹣lnx﹣2,
﹣lnx﹣2,
则f′(x)= ![]() ,
,
令f′(x)>0,解得:x>2,
令f′(x)<0,解得:0<x<2,
∴f(x)在(0,2)递减,在(2,+∞)递增,
∴f(x)≥f(2)=﹣ln2﹣1,
令g(y)=lny﹣2y,
则g′(y)= ![]() ,
,
令g′(y)>0,解得:y< ![]() ,
,
令g′(y)<0,解得:y> ![]() ,
,
∴g(y)在(0, ![]() )递增,在(
)递增,在( ![]() ,+∞)递减,
,+∞)递减,
∴g(y)≤g( ![]() )=﹣ln2﹣1,
)=﹣ln2﹣1,
∴x=2,y= ![]() 时,
时, ![]() ﹣lnx﹣2=lny﹣2y,
﹣lnx﹣2=lny﹣2y,
∴xy= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解对数的运算性质的相关知识,掌握①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() .
.


科目:高中数学 来源: 题型:
【题目】如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点
(1)求证:AC 1//平面CDB1;(2)求证:AC⊥面BB1C1C ;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的左焦点为F,直线y=kx(k>0)与椭圆C交于A,B两点,若
=1(a>b>0)的左焦点为F,直线y=kx(k>0)与椭圆C交于A,B两点,若 ![]() ,则C的离心率取值范围为( )
,则C的离心率取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点. 
(Ⅰ)求证:BF⊥CD;
(Ⅱ)求二面角C﹣BF﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从边长为2a的正方形铁片的四个角各截去一个边长为x的正方形,然后折成一个无盖的长方体盒子,要求长方体的高度x与底面正方形边长的比不超过正数t.
(1)把铁盒的容积V表示为关于x的函数,并指出其定义域.
(2)当x为何值时,容积V有最大值?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,定义域为[0,2π],g(x) 为f(x) 的导函数.
,定义域为[0,2π],g(x) 为f(x) 的导函数.
(1)求方程g(x)=0 的解集;
(2)求函数g(x) 的最大值与最小值;
(3)若函数F(x)=f(x)﹣ax 在定义域上恰有2个极值点,求实数a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用![]() 表示.
表示.
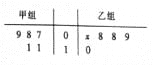
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a、b、c,已知向量 ![]() =(cosA,cosB),
=(cosA,cosB), ![]() =(a,2c﹣b),且
=(a,2c﹣b),且 ![]() ∥
∥ ![]() .
.
(1)求角A的大小;
(2)若a=4,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com