
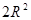 ”,猜测关于球的相应命题由 。
”,猜测关于球的相应命题由 。 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:填空题
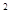 +y
+y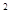 =a
=a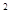 的面积S=
的面积S= a
a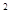 通过类比推理猜想椭圆
通过类比推理猜想椭圆 的面积S=
的面积S= ab. 之后利用演绎推理证明了这个公式是对的! 在平面直角坐标系中, 点集A="{" (x, y)|
ab. 之后利用演绎推理证明了这个公式是对的! 在平面直角坐标系中, 点集A="{" (x, y)|  }, 点集B="{(x," y)|
}, 点集B="{(x," y)|  , 则点集M="{(x," y)|x=x
, 则点集M="{(x," y)|x=x +x
+x , y=y
, y=y +y
+y , (x
, (x , y
, y )
) A, (x
A, (x , y
, y )
) B}所表示的区域的面积为_____________.
B}所表示的区域的面积为_____________. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.没有一个内角是钝角 | B.有两个内角是钝角 |
| C.有三个内角是钝角 | D.至少有两个内角是钝角 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是自然数,所以
是自然数,所以 是整数.”以上三段推理( )。
是整数.”以上三段推理( )。| A.完全正确 |
| B.推理形式不正确 |
| C.不正确,因为两个“自然数”概念不一致 |
| D.不正确,因为两个“整数”概念不一致 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记这样的
成立,记这样的 的个数为
的个数为 ,则得到一个新数列
,则得到一个新数列 。例如,若数列
。例如,若数列 是1,2,3,……,
是1,2,3,……, ,…,则数列
,…,则数列 是0,1,2,…,
是0,1,2,…, , ….已知对任意的
, ….已知对任意的 ,
, ,则
,则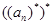 = 。
= 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com