
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2.
(1)若曲线f(x)=xlnx在x=1处的切线与函数g(x)=﹣x2+ax﹣2也相切,求实数a的值;
(2)求函数f(x)在![]() 上的最小值;
上的最小值;
(3)证明:对任意的x∈(0,+∞),都有![]() 成立
成立
【答案】(1)3或-1;(2)见解析;(2)见解析.
【解析】试题分析:(1)求出函数的导数,计算![]() 的值,求出切线方程,再利用判别式为零即可的结果;(2)求出函数的导数,通过讨论
的值,求出切线方程,再利用判别式为零即可的结果;(2)求出函数的导数,通过讨论![]() 的范围,求出函数的单调区间,从而求出
的范围,求出函数的单调区间,从而求出![]() 的最小值即可;(3)设
的最小值即可;(3)设![]() ,求出
,求出![]() 的导数, 求出
的导数, 求出![]() 的最大值,得到
的最大值,得到![]() 恒成立,从而证明结论即可.
恒成立,从而证明结论即可.
试题解析:(1)f′(x)=lnx+x![]() =lnx+1 ,
=lnx+1 ,
![]() 时,
时,![]() ,
,![]() ,
,
故![]() 在
在![]() 处的切线方程是:
处的切线方程是:![]() ,
,
联立![]() ,
,
消去y得:![]() ,
,
由题意得:![]() ,
,
解得:![]() 或
或![]() ;
;
(2)由(1)得:![]() ,
,
x∈(0,![]() )时,
)时,![]() ,
,![]() 递减,
递减,
x∈(![]() ,+∞)时,
,+∞)时, ![]() ,
,![]() 递增,
递增,
①0<t<t+![]() ≤
≤![]() ,即0<t≤
,即0<t≤![]() ﹣
﹣![]() 时,
时,
f(x)min=f(t+![]() )=(t+
)=(t+![]() )ln(t+
)ln(t+![]() ),
),
②0<t<![]() <t+
<t+![]() ,即
,即![]() ﹣
﹣![]() <t<
<t<![]() 时,
时,
f(x)min=f(![]() )=﹣
)=﹣![]() ;
;
③![]() ≤t<t+
≤t<t+![]() ,即
,即![]() 时, f(x)在递增,
时, f(x)在递增,
![]() ;
;
综上,f(x)min=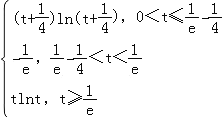 ;
;
(3)证明:设m(x)=![]() ﹣
﹣![]() ,(x∈(0,+∞)),则m′(x)=
,(x∈(0,+∞)),则m′(x)=![]() ,
,
![]() 时,
时,![]() ,
,![]() 递增,
递增,
![]() 时,
时,![]() ,
,![]() 递减,
递减,
可得m(x)max=m(1)=﹣![]() ,当且仅当
,当且仅当![]() 时取到,
时取到,
由(2)得![]() ,(
,(![]() )的最小值是﹣
)的最小值是﹣![]() ,
,
当且仅当x=![]() 时取到,
时取到,
因此![]() 时,f(x)min≥﹣
时,f(x)min≥﹣![]() ≥m(x)max恒成立,
≥m(x)max恒成立,
又两次最值不能同时取到,
故对任意![]() ,都有
,都有![]() 成立.
成立.
【方法点晴】本题主要考查利用导数求曲线切线、利用导数研究函数的单调性以及不等式证明问题,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


科目:高中数学 来源: 题型:
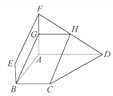
【题目】如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=
90°,BC![]()
![]() AD,BE
AD,BE![]()
![]() FA,G,H分别为FA,FD的中点.
FA,G,H分别为FA,FD的中点.
(1)证明:四边形BCHG是平行四边形.
(2)C,D,F,E四点是否共面?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016~2017·郑州高一检测)过点M(1,2)的直线l与圆C:(x-3)2+(y-4)2=25交于A,B两点,C为圆心,当∠ACB最小时,直线l的方程是 ( )
A. x-2y+3=0 B. 2x+y-4=0
C. x-y+1=0 D. x+y-3=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列![]() 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1-![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①线性回归方程![]() 必过点
必过点![]() ;
;
②在回归方程![]() 中,当变量
中,当变量![]() 增加一个单位时,
增加一个单位时, ![]() 平均增加5个单位;
平均增加5个单位;
③在回归分析中,相关指数![]() 为0.80的模型比相关指数
为0.80的模型比相关指数![]() 为0.98的模型拟合的效果要好;
为0.98的模型拟合的效果要好;
④在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是-7.
的值一定是-7.
其中假命题的个数是 ( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
,![]() 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.
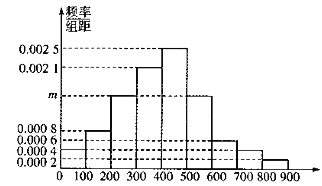
(1)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用![]() 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是![]() 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是![]() .假设各局比赛结果相互独立.
.假设各局比赛结果相互独立.
(1)分别求甲队以3:0,3:1,3:2获胜的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com