
【题目】一个盒子中装有6个完全相同的小球,分别标号为1,2,3,4,5,6.
(1)一次取出两个小球,求其号码之和能被3整除的概率;
(2)有放回的取球两次,每次取一个,求两个小球号码是相邻整数的概率.
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款 | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于![]() 的回归方程
的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数
恰好等于相关系数![]() 的平方,当
的平方,当![]() 时,认为线性回归模型是有效的,请计算
时,认为线性回归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到
并且评价模型的拟合效果(计算结果精确到![]() ).
).
附:
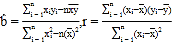 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 过
过![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() (
(![]() 在第二象限).
在第二象限).
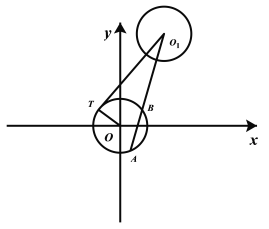
(1)求![]() 的正弦值;
的正弦值;
(2)已知点![]() ,过
,过![]() 点分别作两圆切线,若切线长相等,求
点分别作两圆切线,若切线长相等,求![]() 关系;
关系;
(3)是否存在定点![]() ,使过点
,使过点![]() 有无数对相互垂直的直线
有无数对相互垂直的直线![]() 满足
满足![]() ,且它们分别被圆
,且它们分别被圆![]() 、圆
、圆![]() 所截得的弦长相等?若存在,求出所有的点
所截得的弦长相等?若存在,求出所有的点![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,![]() 平面ABCD,且
平面ABCD,且![]() ,点E为线段PD的中点.
,点E为线段PD的中点.
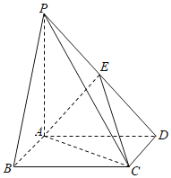
(1)求证:![]() 平面AEC;
平面AEC;
(2)求证:![]() 平面PCD;
平面PCD;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)当![]() 变化时,试问直线
变化时,试问直线![]() 是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语音交互是人工智能的方向之一,现在市场上流行多种可实现语音交互的智能音箱,它们可以通过语音交互满足人们的部分需求.经市场调查,某种新型智能音箱的广告费支出x(万元)与销售额y(单位:万元)之间有如下对应数据:
x | 1 | 4 | 5 | 6 | 9 |
y | 20 | 35 | 50 | 65 | 80 |
(1)求y关于x的线性回归方程(数据精确到0.01);
(2)利用(1)中的回归方程,预测广告费支出10万元时的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为: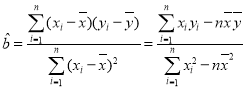 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 是奇函数.
是奇函数.
(1)判断函数![]() 的奇偶性,并求实数
的奇偶性,并求实数![]() 的值;
的值;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若存在
,若存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任为了对本班学生的月考成绩进行分析,从全班40名同学中随机抽取一个容量为6的样本进行分析.随机抽取6位同学的数学、物理分数对应如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学分数x | 60 | 70 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 80 | 88 | 90 | 85 | 95 |
(1)根据上表数据用散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?
(2)如果具有线性相关性,求出线性回归方程(系数精确到0.1);如果不具有线性相关性,请说明理由.
(3)如果班里的某位同学数学成绩为50,请预测这位同学的物理成绩。
![]() (附
(附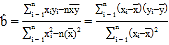 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com