
【题目】数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( ) 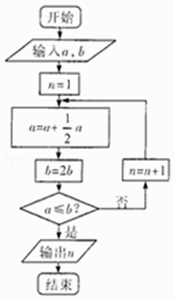
A.4
B.5
C.6
D.7
【答案】B
【解析】解:模拟程序的运行,可得 a=16,b=4,n=1,
a=24,b=8,
不满足循环的条件a≤b,执行循环体,n=2,a=36,b=16
不满足循环的条件a≤b,执行循环体,n=3,a=54,b=32
不满足循环的条件a≤b,执行循环体,n=4,a=81,b=64
不满足循环的条件a≤b,执行循环体,n=5,a= ![]() ,b=128
,b=128
满足循环的条件a≤b,退出循环,输出n的值为5.
故选:B.
【考点精析】关于本题考查的程序框图,需要了解程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 和
和![]() 是全等的等腰梯形,其中
是全等的等腰梯形,其中![]() ,且
,且![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点.
的中点.
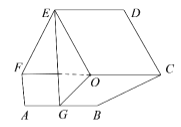
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)请在图中所给的点中找出两个点,使得这两点所在的直线与平面![]() 垂直,并给出证明;
垂直,并给出证明;
(Ⅲ)在线段![]() 上是否存在点,使得
上是否存在点,使得![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆方程;
(2)设不过原点![]() 的直线
的直线![]() ,与该椭圆交于
,与该椭圆交于![]() 两点,直线
两点,直线![]() 的斜率依次为
的斜率依次为![]() ,满足
,满足![]() ,试问:当
,试问:当![]() 变化时,
变化时,![]() 是否为定值?若是,求出此定值,并证明你的结论;若不是请说明理由.
是否为定值?若是,求出此定值,并证明你的结论;若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的交点为F,准线为l,过点F的直线与抛物线交于M,N两点,若MR⊥l,垂足为R,且∠NRM=∠NMR,则直线MN的斜率为( )
A.±8
B.±4
C.±2 ![]()
D.±2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形ABCD如图(1)所示,其中∠ACD=60°,AB=2,AC与BD相交于点O,现沿AC进行翻折,使得平面ACD⊥平面ABC,取点E,连接AE,BE,CE,DE,使得线段BE再平面ABC内的投影落在线段OB上,得到的图形如图(2)所示,其中∠OBE=60°,BE=2. 
(Ⅰ)证明:DE⊥AC;
(Ⅱ)求二面角A﹣BE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移![]() 个单位长度,再向上平移1个单位长度,得到函数y=g(x)的图象.求y=g(x)在区间[0,10π]上零点的个数.
个单位长度,再向上平移1个单位长度,得到函数y=g(x)的图象.求y=g(x)在区间[0,10π]上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,点M(m, 0)在x轴的正半轴上,过M点的直线
,点M(m, 0)在x轴的正半轴上,过M点的直线![]() 与抛物线 C相交于A,B两点,O为坐标原点.
与抛物线 C相交于A,B两点,O为坐标原点.
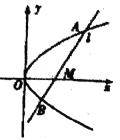
(1) 若m=l,且直线![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2) 是否存在定点M,使得不论直线![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com