
| A. | $-\frac{{2\sqrt{2}}}{9}$ | B. | $-\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{{4\sqrt{2}}}{9}$ | D. | $-\frac{4}{9}$ |
分析 由已知利用诱导公式可求sinα,利用同角三角函数基本关系式可求cosα,进而利用二倍角的正弦函数公式即可计算得解.
解答 解:∵$cos(\frac{π}{2}-α)=\frac{1}{3}$,$\frac{π}{2}<α<π$,
∴sinα=$\frac{1}{3}$,cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{2\sqrt{2}}{3}$,
∴sin2α=2sinαcosα=2×$\frac{1}{3}×$(-$\frac{2\sqrt{2}}{3}$)=-$\frac{4\sqrt{2}}{9}$.
故选:C.
点评 本题主要考查了诱导公式,同角三角函数基本关系式,二倍角的正弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
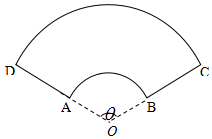 某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{63}$ | B. | $\frac{50}{63}$ | C. | $\frac{43}{63}$ | D. | $\frac{11}{63}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com