
【题目】给定公差大于0的有限正整数等差数列![]() ,其中,
,其中,![]() 为质数.甲、乙两人轮流从
为质数.甲、乙两人轮流从![]() 个石子中取石子,规定:每次每人可取
个石子中取石子,规定:每次每人可取![]() 个石子,取走的石子不再放回,甲先取,取到最后一个石子者为胜.试问:谁有必胜策略?
个石子,取走的石子不再放回,甲先取,取到最后一个石子者为胜.试问:谁有必胜策略?
【答案】见解析
【解析】
设![]() ,其中,
,其中,![]() .
.
令![]() ,
,![]() .
.
那么,当![]() 时,乙有必胜策略;当
时,乙有必胜策略;当![]() 时,甲有必胜策略;当
时,甲有必胜策略;当![]() 时,两人都有不输的策略.
时,两人都有不输的策略.
证明如下:
(1)当![]() 时,乙的策略为:若甲取
时,乙的策略为:若甲取![]() 个石子,则由等差数列的性质,存在
个石子,则由等差数列的性质,存在![]() ,使
,使![]() ,乙取
,乙取![]() 个石子.这样,乙每次都保证他取后剩下的石子数模
个石子.这样,乙每次都保证他取后剩下的石子数模![]() 余0,这使得甲每次都不能使他取后剩下的石子数模
余0,这使得甲每次都不能使他取后剩下的石子数模![]() 余0,从而,甲无法取到最后一个石子.又每次操作,甲、乙合起来共取
余0,从而,甲无法取到最后一个石子.又每次操作,甲、乙合起来共取![]() 个石子,而
个石子,而![]() 是
是![]() 的倍数,若干次操作后,石子全部取走,乙可取到最后一个石子,故乙获胜.
的倍数,若干次操作后,石子全部取走,乙可取到最后一个石子,故乙获胜.
(2)当![]() 时,甲的策略为:先取走
时,甲的策略为:先取走![]() 个石子,则剩下的石子数模
个石子,则剩下的石子数模![]() 余0,转化为前面的情形(1),故甲获胜.
余0,转化为前面的情形(1),故甲获胜.
(3)当![]() 时,证明两人都有不输的策略.
时,证明两人都有不输的策略.
由于![]() ,考察模数列
,考察模数列![]() .
.
因为![]() 的各项互不相同,所以,
的各项互不相同,所以,![]() 的各项互不相同.由此可以断言
的各项互不相同.由此可以断言![]() 的各项不能都属于
的各项不能都属于![]() .
.
否则,![]() 是
是![]() 的一个排列,所以,
的一个排列,所以,
![]() ,即
,即![]() .
.
则![]() .
.
又![]()
![]()
![]() ,
,
可得![]() .故
.故![]() .
.
因为![]() 为质数,所以,
为质数,所以,![]() 或
或![]() .
.
但![]() ,
,![]() ,矛盾,所以,
,矛盾,所以,![]() 中至少有一项,设为
中至少有一项,设为![]() ,它不属于
,它不属于![]() .又由
.又由![]() 可知,
可知,![]() .
.
从而,![]() .
.
由此可见,甲可取![]() 个石子,使剩下的石子数模
个石子,使剩下的石子数模![]() 的余数仍属于
的余数仍属于![]() ,下一次操作无法取走所有石子.
,下一次操作无法取走所有石子.
类似地,乙也有同样的策略,直至无法取出石子,游戏终止.
于是,两人都有不输的策略.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】把![]() ,
,![]() ,
,![]() ,
,![]() 四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,
四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,![]() ,
,![]() 不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .
.
(1)已知椭圆的离心率为![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)已知△![]() 外接圆的圆心在直线
外接圆的圆心在直线![]() 上,求椭圆的离心率
上,求椭圆的离心率![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案的实施,学生对物理学科的选择成了焦点话题. 某学校为了了解该校学生的物理成绩,从![]() ,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到
,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到![]() 班学生物理成绩的频率分布直方图和
班学生物理成绩的频率分布直方图和![]() 班学生物理成绩的频数分布条形图.
班学生物理成绩的频数分布条形图.
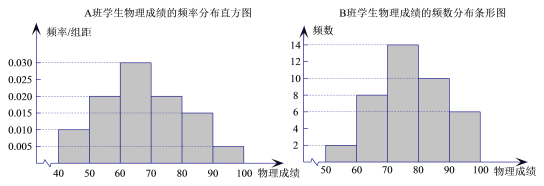
(Ⅰ)估计![]() 班学生物理成绩的众数、中位数(精确到
班学生物理成绩的众数、中位数(精确到![]() )、平均数(各组区间内的数据以该组区间的中点值为代表);
)、平均数(各组区间内的数据以该组区间的中点值为代表);
(Ⅱ)填写列联表,并判断是否有![]() 的把握认为物理成绩与班级有关?
的把握认为物理成绩与班级有关?
物理成绩 | 物理成绩 | 合计 | |
| |||
| |||
合计 |
附:![]() 列联表随机变量
列联表随机变量![]() ;
;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为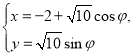 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线![]() 的极坐标方程化为直角坐标方程.
的极坐标方程化为直角坐标方程.
(2)曲线![]() ,
,![]() 是否相交?若相交,请求出公共弦长;若不相交,请说明理由.
是否相交?若相交,请求出公共弦长;若不相交,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com