证明:(Ⅰ)截面MNC
1A
1是等腰梯形,(1分)
连接AC,因为M、N分别为棱AB、BC的中点,
所以MN∥AC,MN≠AC
又AC

A
1C
1,∴MN∥A
1C
1,且MN≠A
1C
1,是梯形,(4分)
易证Rt△AMA
1≌Rt△CNC
1,∴A
1M=C
1N∴MNC
1A
1是等腰梯形(6分)
(Ⅱ)正方体ABCD-A
1B
1C
1D
1中,AC⊥BD,BB
1⊥平面ABCD,MN⊆平面ABCD,∴BB
1⊥MN,又MN∥AC,(8分)
∴MN⊥BD,BD∩BB
1=B,∴MN⊥平面BDD
1B
1,MN⊆平面B
1MN,(10分)
∴平面MNB
1⊥平面BDD
1B
1(12分)
分析:(I)连接AC,因为M、N分别为棱AB、BC的中点,根据MN∥A
1C
1,且MN≠A
1C
1,MNC
1A
1是梯形,易证Rt△AMA
1≌Rt△CNC
1,从而A
1M=C
1N,则MNC
1A
1是等腰梯形;
(Ⅱ)欲证平面MNB
1⊥平面BDD
1B
1,根据面面垂直的判定定理可知在平面B
1MN内一直线与平面平面BDD
1B
1垂直,而根据线面垂直的判定定理可得MN⊥平面BDD
1B
1.
点评:本小题主要考查空间中的线面关系,考查面面垂直的判定及截面图形形状的判定,考查识图能力和推理论证能力,考查转化思想,属于基础题.

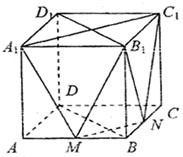 如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱AB,BC的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱AB,BC的中点. A1C1,∴MN∥A1C1,且MN≠A1C1,是梯形,(4分)
A1C1,∴MN∥A1C1,且MN≠A1C1,是梯形,(4分)

 阅读快车系列答案
阅读快车系列答案 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则