
【题目】下列命题是真命题的是( )
A.有两个面相互平行,其余各面都是平行四边形的多面体是棱柱
B.正四面体是四棱锥
C.有一个面是多边形,其余各面都是三角形的多面体叫做棱锥
D.正四棱柱是平行六面体
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点P为双曲线C右支上异于顶点的一点,
,点P为双曲线C右支上异于顶点的一点,![]() 的内切圆与x轴切于点
的内切圆与x轴切于点![]() ,且直线
,且直线![]() 经过线段
经过线段![]() 的中点且垂直于线段
的中点且垂直于线段![]() ,则双曲线C的方程为________________.
,则双曲线C的方程为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某知名电商在![]() 双十一购物狂欢节中成交额再创新高,
双十一购物狂欢节中成交额再创新高,![]() 月
月![]() 日单日成交额达
日单日成交额达![]() 亿元.某店主在此次购物狂欢节期间开展了促销活动,为了解买家对此次促销活动的满意情况,随机抽取了参与活动的
亿元.某店主在此次购物狂欢节期间开展了促销活动,为了解买家对此次促销活动的满意情况,随机抽取了参与活动的![]() 位买家,调查了他们的年龄层次和购物满意情况,得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图:
位买家,调查了他们的年龄层次和购物满意情况,得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图:
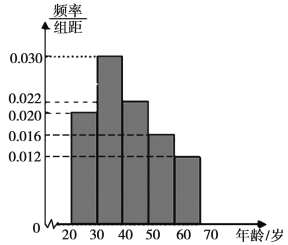
“购物评价为满意”的年龄层次频数分布表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)估计参与此次活动的买家的平均年龄(同一组中的数据用该组区间的中点值做代表);
(2)若年龄在![]() 岁以下的称为“青年买家”,年龄在
岁以下的称为“青年买家”,年龄在![]() 岁以上(含
岁以上(含![]() 岁)的称为“中年买家”,完成下面的列联表,并判断能否有
岁)的称为“中年买家”,完成下面的列联表,并判断能否有![]() 的把握认为中、青年买家对此次活动的评价有差异?
的把握认为中、青年买家对此次活动的评价有差异?
评价满意 | 评价不满意 | 合计 | |
中年买家 | |||
青年买家 | |||
合计 |
|
附:参考公式: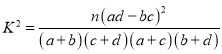 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,
时,![]() 的最小值;
的最小值;
(2)讨论函数的奇偶性,并说明理由;
(3)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意
对任意![]() 恒成立?若存在,求出所有满足条件的
恒成立?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沿海城市的海边有两条相互垂直的直线型公路![]() 、
、![]() ,海岸边界
,海岸边界![]() 近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道
近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段
有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段![]() 是函数
是函数![]() 图像的一段,点M到
图像的一段,点M到![]() 、
、![]() 的距离分别为8千米和1千米,点N到
的距离分别为8千米和1千米,点N到![]() 的距离为10千米,点P到
的距离为10千米,点P到![]() 的距离为2千米.以
的距离为2千米.以![]() 、
、![]() 分别为x,y轴建立如图所示的平面直角坐标系
分别为x,y轴建立如图所示的平面直角坐标系![]() .
.
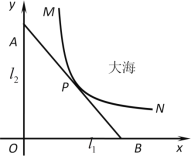
(1)求曲线段![]() 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
(2)求直线![]() 的方程,并求出公路
的方程,并求出公路![]() 的长度(结果精确到1米).
的长度(结果精确到1米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)若![]() ,证明:函数
,证明:函数![]() 在区间
在区间![]() 上是单调增函数;
上是单调增函数;
(2)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若函数![]() 的图像过原点,且
的图像过原点,且![]() 的导数
的导数![]() ,当
,当![]() 时,函数
时,函数![]() 过点
过点![]() 的切线至少有2条,求实数
的切线至少有2条,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某组委会要从五名志愿者中选派四人分别从事翻译导游礼仪司机四项不同工作,若其中甲不能从事翻译工作,乙不能从事导游工作,其余三人均能从事这四项工作,则不同的选派方案共有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,真命题是( )
A.和两条异面直线都相交的两条直线是异面直线
B.和两条异面直线都相交于不同点的两条直线是异面直线
C.和两条异面直线都垂直的直线是异面直线的公垂线
D.若![]() 、
、![]() 是异面直线,
是异面直线,![]() 、
、![]() 是异面直线,则
是异面直线,则![]() 、
、![]() 是异面直线
是异面直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (a>b>0)的离心率e
(a>b>0)的离心率e![]() .
.
(1)若点P(1,![]() )在椭圆E上,求椭圆E的标准方程;
)在椭圆E上,求椭圆E的标准方程;
(2)若D(2,0)在椭圆内部,过点D斜率为![]() 的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com