
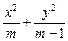 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||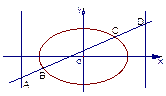
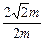 ,m∈[2,5] (2) f(m)的最大值为
,m∈[2,5] (2) f(m)的最大值为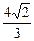 ,此时m=2;f(m)的最小值为
,此时m=2;f(m)的最小值为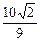 ,此时m=5
,此时m=5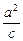 ,即x=±m.
,即x=±m. 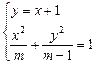 ,消去y得:(m-1)x2+m(x+1)2=m(m-1)
,消去y得:(m-1)x2+m(x+1)2=m(m-1)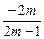 .
.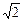 =(xB-xA)·
=(xB-xA)·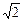 ,|CD|=
,|CD|=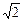 (xD-xC)
(xD-xC)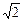 |xB-xA+xD-xC|=
|xB-xA+xD-xC|=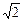 |(xB+xC)-(xA+xD)|
|(xB+xC)-(xA+xD)|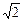 =|
=|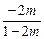 |·
|·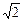 =
=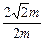 (2≤m≤5)
(2≤m≤5)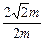 ,m∈[2,5].
,m∈[2,5]. 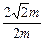 ,可知f(m)=
,可知f(m)=
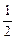 ≤2-
≤2- ≤2-
≤2-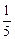 ,∴f(m)∈[
,∴f(m)∈[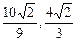 ]
]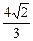 ,此时m=2;f(m)的最小值为
,此时m=2;f(m)的最小值为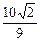 ,此时m=5.
,此时m=5.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:单选题
 (
( )的长轴,若把AB100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、…、P99 ,F1为椭圆的左焦点,则
)的长轴,若把AB100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、…、P99 ,F1为椭圆的左焦点,则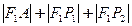 +…
+… 的值是 ( )
的值是 ( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
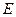 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过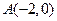 、
、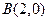 、
、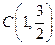 三点.
三点.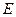 的方程:
的方程: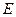 上不同于
上不同于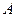 、
、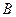 的任意一点,
的任意一点,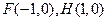 ,当
,当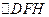 内切圆的面积最大时。求内切圆圆心的坐标;
内切圆的面积最大时。求内切圆圆心的坐标;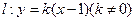 与椭圆
与椭圆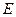 交于
交于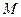 、
、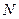 两点,证明直线
两点,证明直线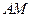 与直线
与直线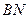 的交点在直线
的交点在直线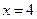 上.
上.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
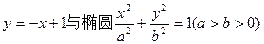 相交于
相交于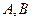 两点,且
两点,且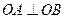 (其中O为坐标原点).
(其中O为坐标原点).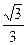 ,求椭圆的标准方程;(2)求证:不论
,求椭圆的标准方程;(2)求证:不论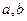 如何变化,椭圆恒过第一象限内的一个定点
如何变化,椭圆恒过第一象限内的一个定点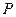 ,并求点
,并求点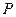 的坐标;(3)若椭圆的离心率
的坐标;(3)若椭圆的离心率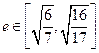 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com