
【题目】若函数f(x)= ![]() x3﹣
x3﹣ ![]() ax2+(a﹣1)x+1在区间(2,3)内为减函数,在区间(5,+∞)为增函数,则实数a的取值范围是( )
ax2+(a﹣1)x+1在区间(2,3)内为减函数,在区间(5,+∞)为增函数,则实数a的取值范围是( )
A.[3,4]
B.[5,7]
C.[4,6]
D.[7,8]
【答案】C
【解析】解:由f(x)= ![]() x3﹣
x3﹣ ![]() ax2+(a﹣1)x+1得f′(x)=x2﹣ax+a﹣1, 令f′(x)=0,解得x=1或x=a﹣1.
ax2+(a﹣1)x+1得f′(x)=x2﹣ax+a﹣1, 令f′(x)=0,解得x=1或x=a﹣1.
当a﹣1≤1,即a≤2时,f′(x)在(1,+∞)上大于0,函数f(x)在(1,+∞)上为增函数,不合题意;
当a﹣1>1,即a>2时,f′(x)在(﹣∞,1)上大于0,函数f(x)在(﹣∞,1)上为增函数,
f′(x)在(1,a﹣1)内小于0,函数f(x)在(1,a﹣1)内为减函数,f′(x)在(a﹣1,+∞)内大于0,
函数f(x)在(a﹣1,+∞)上为增函数.
依题意应有:
当x∈(2,3)时,f′(x)<0,
当x∈(5,+∞)时,f′(x)>0.
∴3≤a﹣1≤5,解得4≤a≤6.
∴a的取值范围是[4,6].
故选:C.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】随着“全面二孩”政策推行,我市将迎来生育高峰。今年新春伊始,泉城各医院产科就已经是一片忙碌至今热度不减。卫生部门进行调查统计期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中10个是“二孩”宝宝;
(1)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询,
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(II)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
P(k≥k市) | 0.40 | 0.25 | 0.15 | 0.10 |
k市 | 0.708 | 1.323 | 2.072 | 2.706 |
K2=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a是实数,函数f(x)=x2(x﹣a). (Ⅰ)若f′(1)=3,求a的值及曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)在区间[0,2]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移 ![]() 个单位长度后得到函数f(x)的图象
个单位长度后得到函数f(x)的图象
(1)写出函数f(x)的解析式;
(2)若对任意的x∈[﹣ ![]() ,
, ![]() ],f2(x)﹣mf(x)﹣1≤0恒成立,求实数m的取值范围;
],f2(x)﹣mf(x)﹣1≤0恒成立,求实数m的取值范围;
(3)求实数a和正整数n,使得F(x)=f(x)﹣a在[0,nπ]上恰有2017个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】机器人![]() (阿法狗)在下围棋时,令人称道的算法策略是:每一手棋都能保证在接下来的十几步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.
(阿法狗)在下围棋时,令人称道的算法策略是:每一手棋都能保证在接下来的十几步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.
下面的算法是寻找“![]() ”中“比较大的数
”中“比较大的数![]() ”,现输入正整数“42,61,80,12,79,18,82,57,31,18“,从左到右依次为
”,现输入正整数“42,61,80,12,79,18,82,57,31,18“,从左到右依次为![]() ,其中最大的数记为
,其中最大的数记为![]() ,则
,则![]() ( )
( )
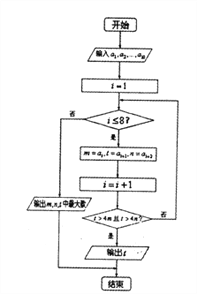
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sinx,
=(sinx, ![]() cosx),
cosx), ![]() =(﹣1,1),
=(﹣1,1), ![]() =(1,1),其中x∈(0,π].
=(1,1),其中x∈(0,π].
(1)若( ![]() +
+ ![]() )∥
)∥ ![]() ,求实数x的值;
,求实数x的值;
(2)若 ![]()
![]() =
= ![]() ,求函数sinx的值.
,求函数sinx的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,k),
=(sinx,k), ![]() =(﹣2cosx,sinx﹣k).
=(﹣2cosx,sinx﹣k).
(1)当x∈[0, ![]() ]时,求|
]时,求| ![]() +
+ ![]() |的取值范围;
|的取值范围;
(2)若g(x)=( ![]() +
+ ![]() )
) ![]() ,求当k为何值时,g(x)的最小值为﹣
,求当k为何值时,g(x)的最小值为﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行六面体ABCD﹣A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( ) 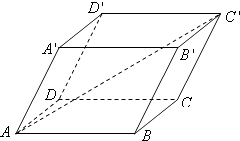
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的方程为y2=10x,直线l的参数方程为 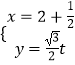 (t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程和直线l的普通方程;
(2)设直线l与曲线C交于A、B两点,求弦长|AB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com