
【题目】设函数f(x)=|x﹣2|+|x+a|(a∈R).
(1)若a=1时,求不等式f(x)≥4的解集;
(2)若不等式f(x)≤2x的解集为[1,+∞),求a的值.
【答案】
(1)解:a=1时,f(x)≥4可化为|x﹣2|+|x+1|≥4.
x<﹣1时,2﹣x﹣x﹣1≥4,∴x≤﹣ ![]() ;
;
﹣1≤x≤2时,2﹣x+x+1≥4,无解;
x>2时,x﹣2+x+1≥4,∴x≥ ![]() .
.
综上所述,不等式的解集为{x|x≤﹣ ![]() 或x≥
或x≥ ![]() }
}
(2)解:∵不等式f(x)≤2x的解集为[1,+∞),
∴|x﹣2|+|x+a|=2x的一个根是1,
∴a=0或﹣2.
a=0时,由|x﹣2|+|x|≤2x,解得x≥1,合题意;
a=﹣2时,由2|x﹣2|≤2x,解得x≥1,合题意;
综上所述,a=0或﹣2
【解析】(1)a=1时,f(x)≥4可化为|x﹣2|+|x+1|≥4.去掉绝对值符号解不等式,即可求不等式f(x)≥4的解集;(2)若不等式f(x)≤2x的解集为[1,+∞),则|x﹣2|+|x+a|=2x的一个根是1,求出a,再进行验证,即可求a的值.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 。
。
Ⅰ.求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
Ⅱ.当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
Ⅲ.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,并且图象关于y轴对称,当x≤-1时,y=f(x)的图象是经过点(-2,0)与(-1,1)的射线,又在y=f(x)的图象中有一部分是顶点在(0,2),且经过点(1,1)的一段抛物线.
(1)试求出函数f(x)的表达式,作出其图象;
(2)根据图象说出函数的单调区间,以及在每一个单调区间上函数是增函数还是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)e2x , g(x)=aln(x+1)+ ![]() x2+(3﹣a)x+a(a∈R).
x2+(3﹣a)x+a(a∈R).
(1)当a=9,求函数y=g(x)的单调区间;
(2)若f(x)≥g(x)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() ax2-1-lnx,其中a∈R.
ax2-1-lnx,其中a∈R.
(1)若a=0,求过点(0,-1)且与曲线y=f(x)相切的直线方程;
(2)若函数f(x)有两个零点x1,x2,
① 求a的取值范围;
② 求证:f ′(x1)+f ′(x2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一块地皮![]() ,其中
,其中![]() ,
, ![]() 是直线段,曲线段
是直线段,曲线段![]() 是抛物线的一部分,且点
是抛物线的一部分,且点![]() 是该抛物线的顶点,
是该抛物线的顶点, ![]() 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, ![]() km,
km, ![]() km,
km, ![]() .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形![]() 来建造草坪,其中点
来建造草坪,其中点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() ,
, ![]() 在直线段
在直线段![]() 上,点
上,点![]() 在直线段
在直线段![]() 上,设
上,设![]() km,矩形草坪
km,矩形草坪![]() 的面积为
的面积为![]() km2.
km2.
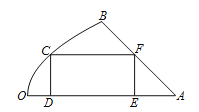
(1)求![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 为多少时,矩形草坪
为多少时,矩形草坪![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如右表,则下列说法正确的是( )
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. 有99.9%的把握认为使用智能手机对学习有影响.
B. 有99.9%的把握认为使用智能手机对学习无影响.
C. 在犯错误的概率不超过0.005的前提下认为使用智能手机对学习有影响.
D. 在犯错误的概率不超过0.005的前提下认为使用智能手机对学习无影响.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中
的组合体中![]() ,
,![]() . 台体体积公式:
. 台体体积公式: ![]() , 其中
, 其中![]() 分别为台体上、下底面面积,
分别为台体上、下底面面积, ![]() 为台体高.
为台体高.
(1)证明:直线![]()
![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
, ![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,求 该组合体的体积.
,求 该组合体的体积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com