
分析 取AB的中点M,分别过A、B、M作准线的垂线AP、BQ、MN,垂足分别为P、Q、N,作出图形,利用抛物线的定义及梯形的中位线性质可推导,|MN|=$\frac{1}{2}$|AB|,从而可判断圆与准线的位置关系.椭圆、双曲线,同理可得.
解答 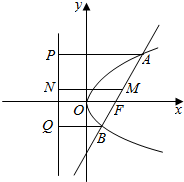 解:取AB的中点M,分别过A、B、M作准线的垂线AP、BQ、MN,垂足分别为P、Q、N,如图所示:
解:取AB的中点M,分别过A、B、M作准线的垂线AP、BQ、MN,垂足分别为P、Q、N,如图所示:
由抛物线的定义可知,|AP|=|AF|,|BQ|=|BF|,
在直角梯形APQB中,|MN|=$\frac{1}{2}$(|AP|+|BQ|)=$\frac{1}{2}$(|AF|+|BF|)=$\frac{1}{2}$|AB|,
故圆心M到准线的距离等于半径,
∴以AB为直径的圆与抛物线的准线相切.
圆半径为r,则r=$\frac{1}{2}$AB,分别过点A,B做右准线的垂线,则构成一个直角梯形,两底长分别为$\frac{1}{e}$AF,$\frac{1}{e}$BF(e为离心率)
圆心到准线的距离d为梯形的中位线长即$\frac{1}{2e}$(AF+BF)
∵椭圆0<e<1,∴d=$\frac{1}{2e}$(AF+BF)=$\frac{1}{2e}$AB>$\frac{1}{2}$AB=r,∴相离
双曲线e>1,可得d<r,相交.
点评 本题考查直线与抛物线、椭圆、双曲线的位置关系、直线圆的位置关系,考查抛物线、椭圆、双曲线的定义,考查数形结合思想,属中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$和y=$(\sqrt{x})^{2}$ | B. | y=lg(x2-1)和y=lg(x+1)+lg(x-1) | ||
| C. | y=logax2和y=2logx | D. | y=x和y=logaax |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3与7 | B. | 2与3 | C. | 2与7 | D. | 3与7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com