
【题目】在平面直角坐标系xOy中,点F是椭圆C:![]() 1(a>b>0)的一个焦点,点D是椭圆上的一个动点,且|FD|∈[1,3].
1(a>b>0)的一个焦点,点D是椭圆上的一个动点,且|FD|∈[1,3].
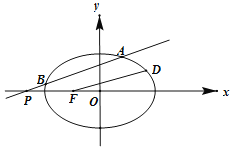
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点P(﹣4,0)作直线交椭圆C于A,B两点,求△AOB面积的最大值.
【答案】(Ⅰ):![]() 1;(Ⅱ)2
1;(Ⅱ)2![]() .
.
【解析】
(Ⅰ)由点![]() 是椭圆上的一个动点,且
是椭圆上的一个动点,且![]() 可得:
可得:![]() 可解得:
可解得:![]() 即可求得椭圆的标准方程;
即可求得椭圆的标准方程;
(Ⅱ)设![]() 由题意设直线
由题意设直线![]() 的方程为
的方程为![]() ,联立
,联立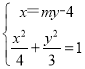
,得![]() ,由韦达定理、点到直线距离公式等,结合已知条件能求出
,由韦达定理、点到直线距离公式等,结合已知条件能求出![]() 面积的最大值.
面积的最大值.
(Ⅰ)由点D是椭圆上的一个动点,且|FD|∈[1,3]可得:a﹣c=1,a+c=3,a2=b2+c解得:a2=4,b2=3,
所以椭圆的标准方程:![]() 1;
1;
(Ⅱ)显然直线AB的斜率不为零,设直线AB的方程:x=my﹣4,A(x,y),B(x',y'),
联立与椭圆的方程整理得:(4+3m2)y2﹣24my+36=0,
△=(﹣24m)2﹣436(4+3m2)>0,整理得m2>4,且y+y'![]() ,yy'
,yy'![]() ,
,
∴|AB|![]() 12
12![]()
O到直线AB的距离d![]() ,
,
所以S△AOB![]() |AB|d=48
|AB|d=48![]() 48
48 2
2![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
所以△AOB面积的最大值:2![]() .
.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成书于公元一世纪的我国经典数学著作《九章算术》中有这样一道名题,就是“引葭赴岸”问题,题目是:“今有池方一丈,点生其中央,出水一尺,引葭赶岸,适马岸齐,问水深,葭长各几何?”题意是:有一正方形池塘,边长为一丈(10尺),有棵芦苇长在它的正中央,高出水面部分有1尺长,把芦苇拉向岸边,恰好碰到沿岸(池塘一边的中点),则水深为__________尺,芦苇长__________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
(1)求这1000名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表. 请将列联表补充完整,并根据列联表判断是否有![]() 的把握认为潜伏期与患者年龄有关;
的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) |
| ||
50岁以下 | 55 | ||
总计 | 200 |
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立. 为了深入研究,该研究团队随机调查了![]() 名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
|
|
| |
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是圆O:x2+y2=4上一动点,过点A作AB⊥x轴,垂足为B,动点D满足![]() .
.
(1)求动点D的轨迹C的方程;
(2)垂直于x轴的直线M交轨迹C于M、N两点,点P(3,0),直线PM与轨迹C的另一个交点为Q.问:直线NQ是否过一定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原来面积为![]() ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的![]() ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的![]() .
.
(1)到今年为止,该森林已砍伐了多少年?
(2)今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有![]() 名学生,其中男生
名学生,其中男生![]() 人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了
人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了![]() 名学生进行调查,月消费金额分布在
名学生进行调查,月消费金额分布在![]() 之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示:
之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示:
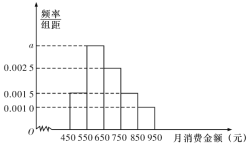
将月消费金额不低于![]() 元的学生称为“高消费群”.
元的学生称为“高消费群”.
(1)求![]() 的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);
的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);
(2)现采用分层抽样的方式从月消费金额落在![]() ,
,![]() 内的两组学生中抽取
内的两组学生中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,记被抽取的
人,记被抽取的![]() 名学生中属于“高消费群”的学生人数为随机变量
名学生中属于“高消费群”的学生人数为随机变量![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)若样本中属于“高消费群”的女生有![]() 人,完成下列
人,完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该校学生属于“高消费群”与“性别”有关?
的把握认为该校学生属于“高消费群”与“性别”有关?
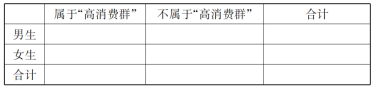
(参考公式: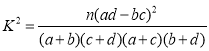 ,其中
,其中![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com