
【题目】已知a=﹣2 ![]() sin(x+
sin(x+ ![]() )dx,求二项式(x2+
)dx,求二项式(x2+ ![]() )5的展开式中x的系数及展开式中各项系数之和.
)5的展开式中x的系数及展开式中各项系数之和.
【答案】解:依题意,a=﹣2 ![]() sin(x+
sin(x+ ![]() )dx=2
)dx=2 ![]() =2
=2 ![]() =﹣2,
=﹣2,
∴二项式(x2+ ![]() )5=
)5= ![]() ,
,
展开式中x的系数及展开式中各项系数之和.
设展开式中含x的项是第r+1项,则Tr+1= ![]() (x2)5﹣r
(x2)5﹣r![]() =(﹣2)r
=(﹣2)r![]() x10﹣3r ,
x10﹣3r ,
令10﹣3r=1,则r=3.∴展开式中x的系数是: ![]() =﹣80.
=﹣80.
令x=1,则二项式的展开式中各项系数之和是(1﹣2)5=﹣1.
【解析】利用微积分基本定理可得a,再利用二项式定理的通项公式及其性质即可得出.
【考点精析】利用定积分的概念对题目进行判断即可得到答案,需要熟知定积分的值是一个常数,可正、可负、可为零;用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限.


科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:f′(x)>1﹣f(x),f(0)=3,f′(x)是f(x)的导函数,则不等式exf(x)>ex+2(其中e为自然对数的底数)的解集为( )
A.{x|x>0}
B.{x|x<0}
C.{x|x<﹣1或x>1}
D.{x|x<﹣1或0<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从吉安市某校高一的1000名学生随机抽取50名分析期中考试数学成绩,被抽取学生成绩全部介于95分和135分之间,将抽取的成绩分成八组:第一组[95,100],第二组[100,105],…,第八组[130,135],如图是按上述分组得到的频率分布直方图的一部分,已知前三组的人数成等差数列,第六组的人数为4人,第一组的人数是第七组、第八组人数之和. 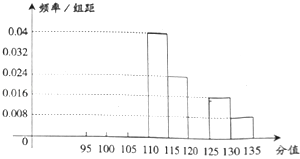
(1)在图上补全频率分布直方图,并估计该校1000名学生中成绩在120分以上(含120分)的人数;
(2)若从成绩属于第六组,第八组的所有学生中随机抽取两名学生,记他们的成绩分别为x,y,事件G=||x﹣y|≤5|,求P(G).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】富华中学的一个文学兴趣小组中,三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究,并且他们选择的名家各不相同.三位同学一起来找图书管理员刘老师,让刘老师猜猜他们三人各自的研究对象.刘老师猜了三句话:“①张博源研究的是莎士比亚;②刘雨恒研究的肯定不是曹雪芹;③高家铭自然不会研究莎士比亚.”很可惜,刘老师的这种猜法,只猜对了一句.据此可以推知张博源、高家铭和刘雨恒分别研究的是__________.(A莎士比亚、B雨果、C曹雪芹,按顺序填写字母即可.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x)是二次函数,如图是f′(x)的大致图象,若f(x)的极大值与极小值的和等于 ![]() ,则f(0)的值为( )
,则f(0)的值为( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+![]() |+a|x﹣
|+a|x﹣![]() |.
|.
(Ⅰ)当a=﹣1时,解不等式f(x)≤3x;
(Ⅱ)当a=2时,若关于x的不等式2f(x)+1<|1﹣b|的解集为空集,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是世界读书日,为提高学生对读书的重视,让更多的人畅游于书海中,从而收获更多的知识,某高中的校学生会开展了主题为“让阅读成为习惯,让思考伴随人生”的实践活动,校学生会实践部的同学随即抽查了学校的40名高一学生,通过调查它们是喜爱读纸质书还是喜爱读电子书,来了解在校高一学生的读书习惯,得到如表列联表:
喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合计 | 24 | 16 | 40 |
(Ⅰ)根据如表,能否有99%的把握认为是否喜欢读纸质书籍与性别有关系?
(Ⅱ)从被抽查的16名不喜欢读纸质书籍的学生中随机抽取2名学生,求抽到男生人数ξ的分布列及其数学期望E(ξ).
参考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心为M(﹣1,2),直线y=x+4被圆M截得的弦长为 ![]() ,点P在直线l:y=x﹣1上.
,点P在直线l:y=x﹣1上.
(1)求圆M的标准方程;
(2)设点Q在圆M上,且满足 ![]() =4
=4 ![]() ,求点P的坐标;
,求点P的坐标;
(3)设半径为5的圆N与圆M相离,过点P分别作圆M与圆N的切线,切点分别为A,B,若对任意的点P,都有PA=PB成立,求圆心N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com