
【题目】已知四棱锥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
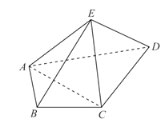
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,求直线
时,求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为等边三角形,其中O为BC中点,且
为等边三角形,其中O为BC中点,且![]() .
.
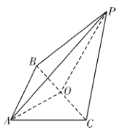
(1)求证:平面![]() 平面PBC;
平面PBC;
(2)若![]() 且
且![]() 平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
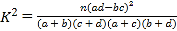 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
B.![]() 是
是![]() 的充要条件
的充要条件
C.设![]() ,则
,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
D.设![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上任意一点P向x轴作垂线段,垂足为Q,点M是线段
上任意一点P向x轴作垂线段,垂足为Q,点M是线段![]() 上的一点,且满足
上的一点,且满足![]()
(1)求点M的轨迹C的方程;
(2)设直线![]() 与轨迹c交于
与轨迹c交于![]() 两点,T为C上异于
两点,T为C上异于![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com