
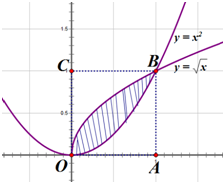
 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 根据积分的几何意义求出阴影区域的面积,然后根据几何概型的概率公式即可得到结论.
解答 解:根据积分的几何意义可知区域M的面积为${∫}_{0}^{1}(\sqrt{x}-{x}^{2})dx$=($\frac{2}{3}{x}^{\frac{3}{2}}-\frac{1}{3}{x}^{3}$)${|}_{0}^{1}$=$\frac{1}{3}$,
区域D的面积为1×1=1,
则由几何概型的概率公式可得点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率等于$\frac{1}{3}$,
故选:B.
点评 本题主要考查几何概型的概率的计算,利用积分的几何意义求出阴影区域的面积是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=0 | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{4}$ | D. | x=$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 类比推理 | B. | 演绎推理 | C. | 归纳推理 | D. | 传递性推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
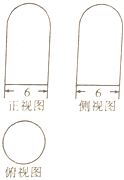 某建筑物是由一个半球和一个圆柱组成,半球的体积是圆柱体积的$\frac{1}{4}$,其三视图如图所示,现需要在该建筑物表面涂一层防晒涂料,若每π个平方单位所需涂料费用为100元,则共需涂料费用( )
某建筑物是由一个半球和一个圆柱组成,半球的体积是圆柱体积的$\frac{1}{4}$,其三视图如图所示,现需要在该建筑物表面涂一层防晒涂料,若每π个平方单位所需涂料费用为100元,则共需涂料费用( )| A. | 6600元 | B. | 7500元 | C. | 8400元 | D. | 9000元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( )
从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( )| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com