
分析 根据向量的加减的几何意义和向量的模计算即可.
解答 解:∵AB=2,AC=3,$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$,
∴$\overrightarrow{AD}$•$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\frac{1}{2}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{1}{4}$(${\overrightarrow{AC}}^{2}$-${\overrightarrow{AB}}^{2}$)=$\frac{1}{4}$(32-22)=$\frac{5}{4}$,
故答案为:$\frac{5}{4}$
点评 本题考查了向量的加减的几何意义和向量的模,属于基础题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
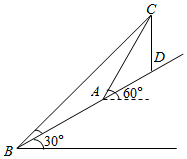 如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为40m,斜坡与水平面成30°角,则铁塔CD的高为$\frac{40\sqrt{3}}{3}$m.
如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为40m,斜坡与水平面成30°角,则铁塔CD的高为$\frac{40\sqrt{3}}{3}$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在某次测量中得到的A样本的茎叶图如图所示,则该样本的中位数、众数、极差分别是( )
在某次测量中得到的A样本的茎叶图如图所示,则该样本的中位数、众数、极差分别是( )| A. | 47,45,56 | B. | 46,45,53 | C. | 45,47,53 | D. | 46,45,56 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
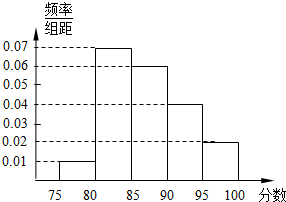 有某单位在2016年的招聘考试中100名竞聘者的笔试成绩,按成绩分组为:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
有某单位在2016年的招聘考试中100名竞聘者的笔试成绩,按成绩分组为:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | $\sqrt{3}$+i | D. | $\sqrt{3}$-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{9}$=1(y≠0) | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) | ||
| C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1(y≠0) | D. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1(y≠0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com