练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图M为的△ABC的中线AD的中点，过M的直线分别与边AB，AC交于点P，Q，设＝x，＝y，记y＝f(x)

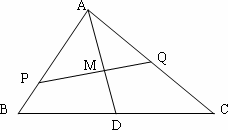
    (1)求函数y＝f(x)的表达式；

    (2)设g(x)＝x3＋3a2x＋2a，(x∈[0，1])，若对于任意x1∈[，1]，总存在x2∈[0，1]使得f(x1)＝g(x2)成立，求实数a的取值范围；

    答案：
    解析：

    　　解：(1)因为过点M的直线分别与两边AB，AC相交所以


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，直角三角形ABC的顶点坐标A（-1，0），直角顶点B(0，-
    		3
    )    ，顶点C在x轴上．
    （1）求△ABC的外接圆M的方程；
    （2）设直线?：y=
    m2+1
    m
    x+
    m2+1
    m
    ，(m∈R，m≠0)    ，直线?能否与圆M相交？为什么？若能相交，直线?能否将圆M分割成弧长的比值为
    1
    2
    的两段弧？为什么？

    查看答案和解析>>

    科目：高中数学 来源：江西省南昌市2012届高三调研测试数学文科试题 题型：044

    如图M为的△ABC的中线AD的中点，过M的直线分别与边AB，AC交于点P，Q，设＝x，＝y记y＝f(x)

    (1)求函数y＝f(x)的表达式；

    (2)设g(x)＝x3＋3a2x＋2a，(x∈[0，1])，若对于任意x1∈[，1]，总存在x2∈[0，1]使得f(x1)＝g(x2)成立，求实数a的取值范围；

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省南通市如皋市高三（上）期中数学试卷（文科）（解析版） 题型：解答题

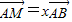    如图，G为△ABC的重心，AD为BC边上的中线．过G的直线MN分别交边AB，AC于M，N两点．设，，记y=f（x）．
    （1）求函数y=f（x）的表达式及其定义域；
    （2）设g（x）=x3+3a2x+2a（x∈[0，1]）．若对任意的，总存在x2∈[0，1]，使得f（x1）=g（x2）成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山东省高三下学期模拟预测文科数学试卷（解析版） 题型：解答题

    如图，平面ABDE⊥平面ABC，ACBC，AC=BC=4，四边形ABDE是直角梯形，BDAE，BD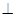BA，AE=2BD=4，O、M分别为CE、AB的中点.

    （Ⅰ）证明：OD//平面ABC；

    （Ⅱ）能否在EM上找一点N，使得ON⊥平面ABDE？若能，请指出点N的位置，并加以证明；若不能，请说明理由.

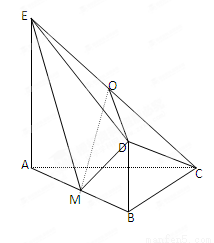
    【解析】第一问：取AC中点F，连结OF、FB.∵F是AC的中点，O为CE的中点，

    ∴OF∥EA且OF=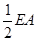且BD=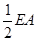

    ∴OF∥DB，OF=DB，

    ∴四边形BDOF是平行四边形。

    ∴OD∥FB

    第二问中，当N是EM中点时，ON⊥平面ABDE。           ………7分

    证明：取EM中点N，连结ON、CM， AC=BC，M为AB中点，∴CM⊥AB，

    又∵面ABDE⊥面ABC，面ABDE面ABC=AB，CM面ABC，

    ∴CM⊥面ABDE，∵N是EM中点，O为CE中点，∴ON∥CM，

    ∴ON⊥平面ABDE。

     

    查看答案和解析>>

    同步练习册答案