
°ĺŐ‚ńŅ°Ņń≥Õ¨—ß‘ŕ—–ĺŅ–‘—ßŌį÷–£¨ ’ľĮĶĹń≥÷∆“©≥ßĹŮńÍ«į5łŲ‘¬ľ◊Ĺļń“…ķ≤ķ≤ķŃŅ£®Ķ•őĽ£ļÕÚļ–£©Ķń żĺ›»ÁŌ¬ĪŪňý ĺ£ļ
‘¬∑›x | 1 | 2 | 3 | 4 | 5 |
y£®ÕÚļ–£© | 4 | 4 | 5 | 6 | 6 |
£®1£©ł√Õ¨—ßő™Ńň«ů≥Ų![]() Ļō”ŕ
Ļō”ŕ![]() ĶńŌŖ–‘ĽōĻť∑Ĺ≥Ő
ĶńŌŖ–‘ĽōĻť∑Ĺ≥Ő![]() £¨łýĺ›ĪŪ÷– żĺ›“—ĺ≠’ż»∑ľ∆ň„≥Ų
£¨łýĺ›ĪŪ÷– żĺ›“—ĺ≠’ż»∑ľ∆ň„≥Ų![]() =0.6£¨ ‘«ů≥Ų
=0.6£¨ ‘«ů≥Ų![]() Ķń÷Ķ£¨≤ĘĻņľ∆ł√≥ß6‘¬∑›…ķ≤ķĶńľ◊Ĺļń“≤ķŃŅ ż£Ľ
Ķń÷Ķ£¨≤ĘĻņľ∆ł√≥ß6‘¬∑›…ķ≤ķĶńľ◊Ĺļń“≤ķŃŅ ż£Ľ
£®2£©»Űń≥“©ĶÍŌ÷”–ł√÷∆“©≥ßĹŮńÍ∂Ģ‘¬∑›…ķ≤ķĶńľ◊Ĺļń“4ļ–ļÕ»ż‘¬∑›…ķ≤ķĶńľ◊Ĺļń“5ļ–£¨–°ļžÕ¨—ßī”÷–ňśĽķĻļ¬ÚŃň3ļ–ľ◊Ĺļń“£¨ļůĺ≠ŃňĹ‚∑ĘŌ÷ł√÷∆“©≥ßĹŮńÍ∂Ģ‘¬∑›…ķ≤ķĶńňý”–ľ◊Ĺļń“ĺýīś‘ŕ÷ ŃŅő Ő‚£¨ľ«–°ļžÕ¨—ßňýĻļ¬ÚĶń3ļ–ľ◊Ĺļń“÷–īś‘ŕ÷ ŃŅő Ő‚Ķńļ– żő™¶ő£¨«ů¶őĶń∑÷≤ľŃ–ļÕ ż—ß∆ŕÕŻ°£
°ĺīūįł°Ņ£®1£©![]() £¨6.8£®2£©ľŻĹ‚őŲ
£¨6.8£®2£©ľŻĹ‚őŲ
°ĺĹ‚īū°ŅĹ‚£ļ£®1£©![]() =
=![]() =3£¨
=3£¨![]() £®4+4+5+6+6£©=5£¨
£®4+4+5+6+6£©=5£¨
“ÚŌŖ–‘ĽōĻť∑Ĺ≥Ő![]() =
=![]() x+
x+![]() ĻżĶ„£®
ĻżĶ„£®![]() £¨
£¨![]() £©£¨
£©£¨
°ŗ![]() =
=![]() ©Ā
©Ā![]()
![]() =5©Ā0.6°Ń3=3.2£¨
=5©Ā0.6°Ń3=3.2£¨
°ŗ6‘¬∑›Ķń…ķ≤ķľ◊Ĺļń“Ķń≤ķŃŅ ż£ļ![]() =0.6°Ń6+3.2=6.8£ģ
=0.6°Ń6+3.2=6.8£ģ
£®2£©¶ő=0£¨1£¨2£¨3£¨
P£®¶ő=0£©=![]() =
=![]() £¨P£®¶ő=1£©=
£¨P£®¶ő=1£©=![]() =
=![]() £¨
£¨
P£®¶ő=2£©=![]() =
=![]() £¨P£®¶ő=3£©=
£¨P£®¶ő=3£©=![]() =
=![]() £¨
£¨
∆š∑÷≤ľŃ–ő™
¶ő | 0 | 1 | 2 | 3 |
P |
|
|
|
|
ňý“‘E¶ő=![]() =
=![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©”…ŌŖ–‘ĽōĻť∑Ĺ≥ŐĻżĶ„£®![]() £¨
£¨![]() £©,Ņ…Ķ√
£©,Ņ…Ķ√![]() ,‘Ŕ«ůx=6 Ī∂‘”¶ļĮ ż÷Ķľīő™6‘¬∑›…ķ≤ķĶńľ◊Ĺļń“≤ķŃŅ ż£®2£©Ō»»∑∂®ňśĽķĪšŃŅ»°∑®£ļ¶ő=0£¨1£¨2£¨3£¨‘ŔņŻ”√◊ťļŌ ż«ů∂‘”¶łŇ¬ £¨Ń–ĪŪŅ…Ķ√∑÷≤ľŃ–£¨◊Óļůłýĺ›Ļę Ĺ«ů ż—ß∆ŕÕŻ
,‘Ŕ«ůx=6 Ī∂‘”¶ļĮ ż÷Ķľīő™6‘¬∑›…ķ≤ķĶńľ◊Ĺļń“≤ķŃŅ ż£®2£©Ō»»∑∂®ňśĽķĪšŃŅ»°∑®£ļ¶ő=0£¨1£¨2£¨3£¨‘ŔņŻ”√◊ťļŌ ż«ů∂‘”¶łŇ¬ £¨Ń–ĪŪŅ…Ķ√∑÷≤ľŃ–£¨◊Óļůłýĺ›Ļę Ĺ«ů ż—ß∆ŕÕŻ
‘Ő‚Ĺ‚őŲ£ļĹ‚£ļ£®1£©![]() =
=![]() =3£¨
=3£¨![]() £®4+4+5+6+6£©=5£¨
£®4+4+5+6+6£©=5£¨
“ÚŌŖ–‘ĽōĻť∑Ĺ≥Ő![]() =
=![]() x+
x+![]() ĻżĶ„£®
ĻżĶ„£®![]() £¨
£¨![]() £©£¨
£©£¨
°ŗ![]() =
=![]() ©Ā
©Ā![]()
![]() =5©Ā0.6°Ń3=3.2£¨
=5©Ā0.6°Ń3=3.2£¨
°ŗ6‘¬∑›Ķń…ķ≤ķľ◊Ĺļń“Ķń≤ķŃŅ ż£ļ![]() =0.6°Ń6+3.2=6.8£ģ
=0.6°Ń6+3.2=6.8£ģ
£®2£©¶ő=0£¨1£¨2£¨3£¨
P£®¶ő=0£©=![]() =
=![]() £¨P£®¶ő=1£©=
£¨P£®¶ő=1£©=![]() =
=![]() £¨
£¨
P£®¶ő=2£©=![]() =
=![]() £¨P£®¶ő=3£©=
£¨P£®¶ő=3£©=![]() =
=![]() £¨
£¨
∆š∑÷≤ľŃ–ő™
¶ő | 0 | 1 | 2 | 3 |
P |
|
|
|
|
ňý“‘E¶ő=![]() =
=![]() £ģ
£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ’Ň ¶łĶŌŽ“™“ĽłŲ»ÁÕľ1ňý ĺĶńł÷ĹÓ÷ßľ‹Ķń◊ťļŌŐŚ£¨ņīĶĹ“Ľľ“ł÷÷∆∆∑ľ”Ļ§ĶÍ∂®÷∆£¨ń√≥Ų◊‘ľļĽ≠Ķń◊ťļŌŐŚ»ż ”Õľ£®»ÁÕľ2ňý ĺ£©.ĶÍņŌįŚŅīŃň»ż ”Õľ£¨Ī®Ńň◊ÓĶÕľŘ£¨’Ň ¶łĶĺűĶ√ļ‹Ī„“ň£¨ĶĪľīň¶Ō¬∂®ĹūļÕ»ż ”Õľ£¨‘ľ∂®Ķŕ∂ĢŐžŐŠĽű.Ķŕ∂ĢŐžŐŠĽű Ī£¨ĶÍņŌįŚ“ĽŃ≥ĽĶ–¶ĶńŇű≥Ų»ÁÕľ3®C1ňý ĺĶń◊ťļŌŐŚ£¨’Ň ¶łĶ“ĽŅī£¨Ń≥∂ľ¬ŐŃň£ļ°įľť…Ő£¨‘űń‹»ÁīňÕĶĻ§ľűŃŌ°Ī.ĶÍņŌįŚňĶ£¨ő“ «įīń„Ķń»ż ”Õľ◊ŲĶń£¨“™≤Ľő“łÝń„ľ”“ĽłŲ’ż∑ĹŐŚ£¨Ķę“™ľ”ľŘ£¨ňśĽķľ”…ŌŃň“ĽłŲ’ż∑ĹŐŚ£¨Ķ√ĶĹ»ÁÕľ3®C2ňý ĺĶń◊ťļŌŐŚ£Ľ’Ň ¶łĶŃ≥ĽĻ «¬ŐĶń£¨ĶÍņŌįŚ”÷ľ”…Ō“ĽłŲ’ż∑ĹŐŚ£¨◊ť≥…Ńň»ÁÕľ 3®C3 ňý ĺĶń◊ťļŌŐŚ£¨”÷ľ”ľŘ£Ľ’Ň ¶łĶŃ≥ľŐ–Ý¬Ő£¨ĶÍņŌįŚ‘Ŕľ”“ĽłŲ’ż∑ĹŐŚ£¨◊ť≥…»ÁÕľ 3®C4 ňý ĺĶń◊ťļŌŐŚ£¨‘Ŕīőľ”ľŘ£Ľňę∑ĹĺÕ»ż ”Õľ’ý≥≥≤Ľ–›°≠°≠


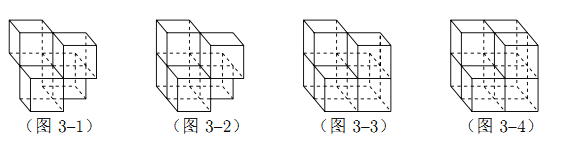
ń„»Ōő™ĶÍņŌįŚŐŠĻ©Ķń![]() łŲ◊ťļŌŐŚĶń»ż ”Õľ”Ž’Ň ¶łĶĽ≠Ķń»ż ”Õľ“Ľ÷¬ĶńłŲ ż «£® £©
łŲ◊ťļŌŐŚĶń»ż ”Õľ”Ž’Ň ¶łĶĽ≠Ķń»ż ”Õľ“Ľ÷¬ĶńłŲ ż «£® £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™![]() £¨ļĮ ż
£¨ļĮ ż![]() .
.
£®ĘŮ£©»ŰļĮ ż![]() ‘ŕ
‘ŕ![]() …ŌĶ›ľű, «ů Ķ ż
…ŌĶ›ľű, «ů Ķ ż![]() Ķń»°÷Ķ∑∂őߣĽ
Ķń»°÷Ķ∑∂őߣĽ
£®ĘÚ£©ĶĪ![]() Ī£¨«ů
Ī£¨«ů![]() Ķń◊Ó–°÷Ķ
Ķń◊Ó–°÷Ķ![]() Ķń◊Óīů÷Ķ£Ľ
Ķń◊Óīů÷Ķ£Ľ
£®Ęů£©…Ť![]() £¨«ů÷§£ļ
£¨«ů÷§£ļ![]() .
.

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľňý ĺ£¨ňńĪŖ–őABEFļÕABCD∂ľ «÷ĪĹ«Ő›–ő£¨°ŌBAD=°ŌFAB=
90°„£¨BC![]()
![]() AD£¨BE
AD£¨BE![]()
![]() FA£¨G£¨H∑÷Īūő™FA£¨FDĶń÷–Ķ„.
FA£¨G£¨H∑÷Īūő™FA£¨FDĶń÷–Ķ„.
(1)÷§√ų£ļňńĪŖ–őBCHG «∆Ĺ––ňńĪŖ–ő.
(2)C£¨D£¨F£¨EňńĶ„ «∑ŮĻ≤√ś£Ņő™ ≤√ī£Ņ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() ‘ŕ
‘ŕ![]() ī¶Ķń«–ŌŖő™
ī¶Ķń«–ŌŖő™![]() .
.
(1)«ů![]() ĶńĹ‚őŲ Ĺ.
ĶńĹ‚őŲ Ĺ.
(2)»Ű∂‘»ő“‚![]() £¨”–
£¨”–![]() ≥…ŃĘ£¨«ů Ķ ż
≥…ŃĘ£¨«ů Ķ ż![]() Ķń»°÷Ķ∑∂őß.
Ķń»°÷Ķ∑∂őß.
(3)÷§√ų£ļ∂‘»ő“‚![]() ≥…ŃĘ.
≥…ŃĘ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ŌÚŃŅm£Ĺ(cosx£¨£≠1)£¨n£Ĺ![]() £¨ļĮ żf(x)£Ĺ(m£ęn)°§m.
£¨ļĮ żf(x)£Ĺ(m£ęn)°§m.
(1)«ůļĮ żf(x)Ķń◊Ó–°’ż÷‹∆ŕ£Ľ
(2)“—÷™a£¨b£¨c∑÷Īūő™°ųABCńŕĹ«A£¨B£¨CĶń∂‘ĪŖ£¨Aő™»ŮĹ«£¨a£Ĺ1£¨c£Ĺ![]() £¨«“f(A)«° «ļĮ żf(x)‘ŕ
£¨«“f(A)«° «ļĮ żf(x)‘ŕ![]() …ŌĶń◊Óīů÷Ķ£¨«ůA£¨bļÕ°ųABCĶń√śĽż.
…ŌĶń◊Óīů÷Ķ£¨«ůA£¨bļÕ°ųABCĶń√śĽż.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ–°Õű°Ę–°ņÓŃĹőĽÕ¨—ßÕś÷ņųĽ◊”(ųĽ◊”÷ Ķōĺý‘»)”őŌ∑,Ļś‘Ú:–°ÕűŌ»÷ņ“Ľ√∂ųĽ◊”,ŌÚ…ŌĶńĶ„ żľ«ő™x;–°ņÓļů÷ņ“Ľ√∂ųĽ◊”,ŌÚ…ŌĶńĶ„ żľ«ő™y,
(1)‘ŕ÷ĪĹ«◊ÝĪÍŌĶxOy÷–,“‘(x,y)ő™◊ÝĪÍĶńĶ„Ļ≤”–ľłłŲ? ‘«ůĶ„(x,y)¬š‘ŕ÷ĪŌŖx+y=7…ŌĶńłŇ¬ ;
(2)Ļś∂®:»Űx+y°›10,‘Ú–°Õű”ģ;»Űx+y°‹4,‘Ú–°ņÓ”ģ,∆šňŻ«ťŅŲ≤Ľ∑÷ š”ģ. ‘ő ’‚łŲ”őŌ∑Ļś‘ÚĻę∆Ŭū?«ŽňĶ√ųņŪ”….
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ(2016°ę2017°§÷£÷›łŖ“Ľľž≤‚)ĻżĶ„M(1,2)Ķń÷ĪŌŖl”Ž‘≤C£ļ(x£≠3)2£ę(y£≠4)2£Ĺ25ĹĽ”ŕA£¨BŃĹĶ„£¨Cő™‘≤–ń£¨ĶĪ°ŌACB◊Ó–° Ī£¨÷ĪŌŖlĶń∑Ĺ≥Ő « (°°°°)
A. x£≠2y£ę3£Ĺ0 B. 2x£ęy£≠4£Ĺ0
C. x£≠y£ę1£Ĺ0 D. x£ęy£≠3£Ĺ0
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]()
£®1£©»Ű![]() ő™«ķŌŖ
ő™«ķŌŖ![]() Ķń“ĽŐű«–ŌŖ£¨«ůaĶń÷Ķ£Ľ
Ķń“ĽŐű«–ŌŖ£¨«ůaĶń÷Ķ£Ľ
£®2£©“—÷™![]() £¨»Űīś‘ŕő®“ĽĶń’Ż ż
£¨»Űīś‘ŕő®“ĽĶń’Ż ż![]() £¨ ĻĶ√
£¨ ĻĶ√![]() £¨«ůaĶń»°÷Ķ∑∂őß.
£¨«ůaĶń»°÷Ķ∑∂őß.
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com