
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

【答案】(1) ![]() (2)36000(3)
(2)36000(3)![]()
【解析】试题分析:本题主要考查频率分布直方图、频率、频数的计算等基础知识,考查学生的分析问题、解决问题的能力. 第(Ⅰ)问,由高×组距=频率,计算每组的频率,根据所有频率之和为1,计算出a的值;第(Ⅱ)问,利用高×组距=频率,先计算出每人月均用水量不低于3吨的频率,再利用频率×样本容量=频数,计算所求人数;第(Ⅲ)问,将前5组的频率之和与前4组的频率之和进行比较,得出2≤x<2.5,再估计月均用水量的中位数.
试题解析:(Ⅰ)由频率分布直方图,可知:月均用水量在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5)等组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1–(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,
解得a=0.30.
(Ⅱ)由(Ⅰ),100位居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300 000×0.12="36" 000.
(Ⅲ)设中位数为x吨.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5
所以2≤x<2.5.
由0.50×(x–2)=0.5–0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线![]() 的焦点重合,过点
的焦点重合,过点![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下列命题的否定,并判断真假:
(1)不论![]() 取何实数,方程
取何实数,方程![]() 必有实数根;
必有实数根;
(2)所有末位数字是0或5的整数都能被5整除;
(3)某些梯形的对角线互相平分;
(4)被8整除的数能被4整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校欲在甲、乙两店采购某款投影仪,该投影仪原价为每台2000元,甲店用如下方法促销:买一台单价为1950元,买二台单价为1900元,每多买一台,则所买各台单价均再减50元,但最低不能低于1200元;乙店一律按原售价的80%促销,学校需要购买![]() 台投影仪,若在甲店购买费用为
台投影仪,若在甲店购买费用为![]() 元,若在乙店购买费用记为
元,若在乙店购买费用记为![]() .
.
(1)分别求出![]() 和
和![]() 的解析式;
的解析式;
(2)当购买![]() 台时,在哪家店买更省钱?
台时,在哪家店买更省钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到0.1).
精确到0.1).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为
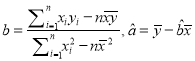 ,相关系数
,相关系数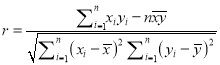
参考数据:
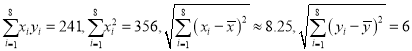 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙3人均以游戏的方式决定是否参加学校音乐社团、美术社团,游戏规则为:
①先将一个圆8等分(如图),再将8个等分点![]() ,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心
,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心![]() 构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
②前一个同学摸出两个小球记录下结果后,把两个小球都放回盒内,下一位同学再从盒中随机摸取两个小球。

(1)求甲能参加音乐社团的概率;
(2)记甲、乙、丙3人能参加音乐社团的人数为随机变量![]() ,求
,求![]() 的分布列、数学期望和方差
的分布列、数学期望和方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com