
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;(2)若对任意的
的值;(2)若对任意的![]() ,都有
,都有![]() 成立,求正数
成立,求正数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】试题分析:(1)求出![]() 的导数,由
的导数,由![]() ,得
,得![]() ;(2)不等式整理可得
;(2)不等式整理可得![]() , 在
, 在![]() 恒成立,利用导数研究函数的单调性,求出函数
恒成立,利用导数研究函数的单调性,求出函数![]() 的最小值,即可得到
的最小值,即可得到![]() 的范围.
的范围.
试题解析:(1)由题意得![]() ,因函数在
,因函数在![]() 处的切线方程为
处的切线方程为![]() ,
,
所以![]() ,得
,得![]() .
.
(2)由(1)知![]() 对任意
对任意![]() 都成立,
都成立, ![]()
又不等式整理可得![]() ,
,
令![]() ,
,
所以 ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
同理,函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
【方法点晴】本题主要考查利用导数求函数的切线斜率以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题是利用方法 ① 求得
恒成立;④ 讨论参数.本题是利用方法 ① 求得![]() 的取值范围.
的取值范围.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
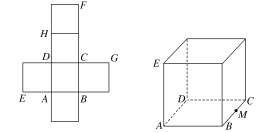
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如下.通过计算,可以得到对应的回归方程![]() =-2.352x+147.767,根据以上信息,判断下列结论中正确的是( )
=-2.352x+147.767,根据以上信息,判断下列结论中正确的是( )
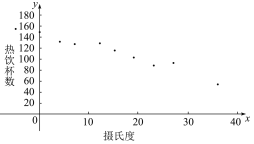
摄氏温度 | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
热饮杯数 | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
A.气温与热饮的销售杯数之间成正相关
B.当天气温为2℃时,这天大约可以卖出143杯热饮
C.当天气温为10℃时,这天恰卖出124杯热饮
D.由于x=0时,![]() 的值与调查数据不符,故气温与卖出热饮杯数不存在线性相关性
的值与调查数据不符,故气温与卖出热饮杯数不存在线性相关性
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的参数方程为![]() (t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(1)求点Q的轨迹C2的直角坐标方程;
(2)直线l与直线C2交于A,B两点,若|AB|≥2![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集为[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在路边安装路灯,路宽为![]() ,灯柱
,灯柱![]() 长为
长为![]() 米,灯杆
米,灯杆![]() 长为1米,且灯杆与灯柱成
长为1米,且灯杆与灯柱成![]() 角,路灯采用圆锥形灯罩,其轴截面的顶角为
角,路灯采用圆锥形灯罩,其轴截面的顶角为![]() ,灯罩轴线
,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直.
垂直.
⑴设灯罩轴线与路面的交点为![]() ,若
,若![]() 米,求灯柱
米,求灯柱![]() 长;
长;
⑵设![]() 米,若灯罩截面的两条母线所在直线一条恰好经过点
米,若灯罩截面的两条母线所在直线一条恰好经过点![]() ,另一条与地面的交点为
,另一条与地面的交点为![]() (如图2)
(如图2)


(图1) (图2)
(ⅰ)求![]() 的值;(ⅱ)求该路灯照在路面上的宽度
的值;(ⅱ)求该路灯照在路面上的宽度![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中学生测评中,分“优秀、合格、尚待改进”三个等级进行学生互评,某校高一年级有男生![]() 人,女生
人,女生![]() 人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了
人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了![]() 名学生的测评结果,并作出频数统计表如下:
名学生的测评结果,并作出频数统计表如下:
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表一:男生
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
表二:女生
(1)从表二的非优秀学生中随机选取![]() 人交谈,求所选
人交谈,求所选![]() 人中恰有
人中恰有![]() 人测评等级为合格的概率;
人测评等级为合格的概率;
(2)由表中统计数据填写![]() 列联表,试采用独立性检验进行分析,能否在犯错误的概率不超过
列联表,试采用独立性检验进行分析,能否在犯错误的概率不超过![]() 的前提下认为“测评结果优秀与性别有关”,参考数据与公示:
的前提下认为“测评结果优秀与性别有关”,参考数据与公示:  ,其中
,其中![]()
临界值表:
| 0.10 | 0.05 | 0.01 |
| 2.70 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是R上的偶函数,且在[0,+∞)上单调递增,则f(-2),f(3),f(-![]() )的大小顺序是:( )
)的大小顺序是:( )
A. f(-![]() )>f(3)>f(-2) B. f(-
)>f(3)>f(-2) B. f(-![]() ) >f(-2)>f(3)
) >f(-2)>f(3)
C. f(-2)>f(3)> f(-![]() ) D. f(3)>f(-2)> f(-
) D. f(3)>f(-2)> f(-![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com