在等差数列{an}中,7a5+5a9=0,且a5<a9,则使该数列前n项和Sn取得最小值时的n= .
【答案】
分析:根据题意先求出数列的公差,再求出通项公式,令a
n≥0,求出n的范围,判断出从第几项开始为正项,即可判断出数列的前n项和S
n最小.
解答:解:设等差数列{a
n}的公差为d,∵a
9>a
5,∴4d>0即d>0
又∵7a
5+5a
9=0,∴7(a
1+4d)+5(a
1+8d)=0
∴3a
1+17d=0,∴a
1=
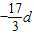
<0
∴a
n=a
1+(n-1)d=
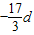
+(n-1)d=(n-
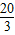
)d
令(n-
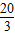
)d≥0,解得n
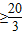
,
故等差数列{a
n}中,前6项均为负值,从第7项开始全为正数,
故当n=6时,该数列前n项和S
n取得最小值,
故答案为:6
点评:本题考查了等差数列前n项和S
n的性质,正确表示数列的通项公式是解决问题的关键,属基础题.

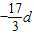 <0
<0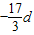 +(n-1)d=(n-
+(n-1)d=(n-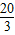 )d
)d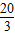 )d≥0,解得n
)d≥0,解得n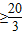 ,
,

 名校课堂系列答案
名校课堂系列答案