
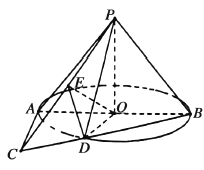
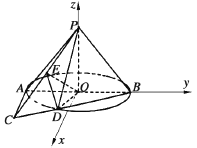
【题目】如图,在以![]() 为顶点,母线长为
为顶点,母线长为![]() 的圆锥中,底面圆
的圆锥中,底面圆![]() 的直径
的直径![]() 长为2,
长为2,![]() 是圆
是圆![]() 所在平面内一点,且
所在平面内一点,且![]() 是圆
是圆![]() 的切线,连接
的切线,连接![]() 交圆
交圆![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,当二面角
,当二面角![]() 的大小为
的大小为![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由![]() 是圆
是圆![]() 的直径,
的直径,![]() 与圆
与圆![]() 切于点
切于点![]() ,可得
,可得![]() ,
,
由![]() 底面圆
底面圆![]() ,可得
,可得![]() ,利用线面垂直的判定定理可知,
,利用线面垂直的判定定理可知,![]() 平面
平面![]() ,即可推出
,即可推出![]() .又在
.又在![]() 中,
中,![]() ,可推出
,可推出![]() ,利用线面垂直的判定定理可证
,利用线面垂直的判定定理可证![]() 平面
平面![]() ,从而利用面面垂直的判定定理可证出平面
,从而利用面面垂直的判定定理可证出平面![]() 平面
平面![]() .
.
(2)由![]() ,
,![]() ,可知
,可知![]() 为二面角
为二面角![]() 的平面角,
的平面角,
即![]() ,建立空间直角坐标系,易知
,建立空间直角坐标系,易知![]() ,
,
求得点的坐标如下;![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,
,
![]() ,
,![]() ,
,
通过![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
可求出平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴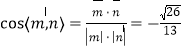 .
.
∴ 平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
解:(1)![]() 是圆
是圆![]() 的直径,
的直径,![]() 与圆
与圆![]() 切于点
切于点![]() ,
,![]()
![]() 底面圆
底面圆![]() ,∴
,∴![]()
![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵在![]() 中,
中,![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() 平面
平面![]() ,从而平面
,从而平面![]() 平面
平面![]() .
.
(2)∵ ![]() ,
,![]() ,∴
,∴![]() 为二面角
为二面角![]() 的平面角,
的平面角,
∴ ![]() ,
,
如图建立空间直角坐标系,易知![]() ,
,
则![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,
,
![]() ,
,![]() ,
,
∵ ![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴ 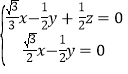 ,即
,即![]()
故平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴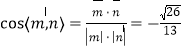 .
.
∴ 平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH中点,PA=AC=2,BC=1.
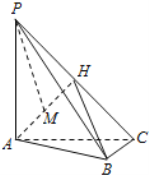
(Ⅰ)求证:AH⊥平面PBC;
(Ⅱ)求PM与平面AHB成角的正弦值;
(Ⅲ)在线段PB上是否存在点N,使得MN∥平面ABC,若存在,请说明点N的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂有![]() 台大型机器,在
台大型机器,在![]() 个月中,
个月中,![]() 台机器至多出现
台机器至多出现![]() 次故障,且每台机器是否出现故障是相互独立的,出现故障时需
次故障,且每台机器是否出现故障是相互独立的,出现故障时需![]() 名工人进行维修.每台机器出现故障的概率为
名工人进行维修.每台机器出现故障的概率为![]() .已知
.已知![]() 名工人每月只有维修
名工人每月只有维修![]() 台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得
台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得![]() 万元的利润,否则将亏损
万元的利润,否则将亏损![]() 万元.该工厂每月需支付给每名维修工人
万元.该工厂每月需支付给每名维修工人![]() 万元的工资.
万元的工资.
(1)若每台机器在当月不出现故障或出现故障时有工人进行维修,则称工厂能正常运行.若该厂只有![]() 名维修工人,求工厂每月能正常运行的概率;
名维修工人,求工厂每月能正常运行的概率;
(2)已知该厂现有![]() 名维修工人.
名维修工人.
(ⅰ)记该厂每月获利为![]() 万元,求
万元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(ⅱ)以工厂每月获利的数学期望为决策依据,试问该厂是否应再招聘![]() 名维修工人?
名维修工人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①一组数据的标准差越大,则说明这组数据越集中;
②曲线![]() 与曲线
与曲线![]() 的焦距相等;
的焦距相等;
③在频率分布直方图中,估计的中位数左边和右边的直方图的面积相等;
④已知椭圆![]() ,过点
,过点![]() 作直线,当直线斜率为
作直线,当直线斜率为![]() 时,M刚好是直线被椭圆截得的弦AB的中点.
时,M刚好是直线被椭圆截得的弦AB的中点.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算K2=8.01,附表如下:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表,得到的正确的结论是( )
A. 有99%以上的把握认为“喜欢乡村音乐与性别有关”
B. 有99%以上的把握认为“喜欢乡村音乐与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,曲线
,曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com