
【题目】甲、乙两人进行某项对抗性游戏,采用“七局四胜”制,即先赢四局者为胜,若甲、乙两人水平相当,且已知甲先赢了前两局.
![]() Ⅰ
Ⅰ![]() 求乙取胜的概率;
求乙取胜的概率;
![]() Ⅱ
Ⅱ![]() 记比赛局数为X,求X的分布列及数学期望
记比赛局数为X,求X的分布列及数学期望![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为xkm,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在的 ![]() 中点时,对城A和城B的总影响度为0.065.
中点时,对城A和城B的总影响度为0.065. 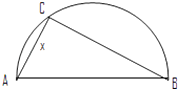
(1)将y表示成x的函数;
(2)讨论(1)中函数的单调性,并判断弧 ![]() 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由.
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)利用分层抽样的方法从善于使用学案的同学中随机抽取6人,从这6人中抽出3人继续调查,设抽出学习成绩优秀的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1、x2、x3、x4,且x1<x2<x3<x4 , 则2(x4﹣x1)+(x3﹣x2)的取值范围是( )
A.(8,6 ![]() )
)
B.(6 ![]() ,4
,4 ![]() )
)
C.[8,4 ![]() ]
]
D.(8,4 ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. 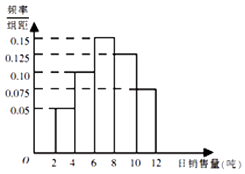
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用X表示未来3天内日销售量不低于8吨的天数,求随机变量X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆![]() 的方程为
的方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)
为参数)
(1)求圆![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与圆
与圆![]() 相切,求实数
相切,求实数![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|cosx|sinx,给出下列五个说法:
①f( ![]() π)=﹣
π)=﹣ ![]() ;
;
②若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z);
③f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
④函数f(x)的周期为π.
⑤f(x)的图象关于点( ![]() ,0)成中心对称.
,0)成中心对称.
其中正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数)M是C1上的动点,P点满足
(α为参数)M是C1上的动点,P点满足 ![]() =2
=2 ![]() ,P点的轨迹为曲线C2
,P点的轨迹为曲线C2
(1)求C2的方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ= ![]() 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com