
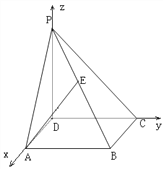
【题目】如图,PD垂直正方形ABCD所在平面,AB=2,E是PB的中点, ![]() ,
, ![]() >
>![]() .
.

(1)建立适当的空间坐标系,求出点E的坐标;
(2)在平面PAD内求一点F,使EF⊥平面PCB.
【答案】(1)点E坐标是(1,1,1)(2)点F的坐标是(1,0,0)
【解析】试题分析:
(1)由题意,分别以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,结合空间中点的坐标,设P(0,0,2m),则![]() (1,1,m),结合平面向量夹角公式得到关于m的方程,解方程可得点E坐标是(1,1,1);
(1,1,m),结合平面向量夹角公式得到关于m的方程,解方程可得点E坐标是(1,1,1);
(2)由题意,设F(x,0,z),结合平面向量的法向量和直线的方向向量得到关于坐标的方程组,求解方程组可得即点F是AD的中点.
试题解析:
(1)分别以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,如图,则
![]() (2,0,0),B(2,2,0),C(0,2,0),
(2,0,0),B(2,2,0),C(0,2,0),
设P(0,0,2m),则![]() (1,1,m),
(1,1,m),
∴ ![]() (-1,1,m),
(-1,1,m),![]() =(0,0,2m)
=(0,0,2m)
∴ ![]() ,
, 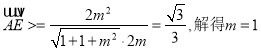 .
.
∴ 点E坐标是(1,1,1);
(2)∵![]() 平面PAD, ∴ 可设F(x,0,z)
平面PAD, ∴ 可设F(x,0,z)
![]() =(x-1,-1,z-1), 又EF⊥平面PCB,
=(x-1,-1,z-1), 又EF⊥平面PCB,
∴ ![]()
![]() ,-1,
,-1, ![]()
![]() 2,0,
2,0, ![]() =0,解得,
=0,解得, ![]() ;
;
又∵![]() ∴
∴ ![]() ,-1,
,-1, ![]() 0,2,-2
0,2,-2![]()
∴ 点F的坐标是(1,0,0),即点F是AD的中点.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知1丈为10尺,该锲体的三视图如图所示,则该锲体的体积为( ) 
A.10000立方尺
B.11000立方尺
C.12000立方尺
D.13000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司购买了一块长AM=30米,宽AN=20米的矩形地块,计划把图中矩形ABCD建设为仓库,其余地方为道路和停车场,要求顶点C在地块对角线MN上,B、D分别在边AM、AN上,假设AB的长度为x米
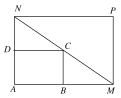
(1)求矩形ABCD的面积S关于x的函数解析式;
(2)要使仓库占地ABCD的面积不少于144平方米,则AB的长度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin(2x+ ![]() )图象上的点M(θ,
)图象上的点M(θ, ![]() )(0<θ<
)(0<θ< ![]() )向右平移t(t>0)个单位长度得到点M′.若M′位于函数y=sin2x的图象上,则( )
)向右平移t(t>0)个单位长度得到点M′.若M′位于函数y=sin2x的图象上,则( )
A.θ= ![]() ,t的最小值为
,t的最小值为 ![]()
B.θ= ![]() ,t的最小值为
,t的最小值为 ![]()
C.θ= ![]() ,t的最小值为
,t的最小值为 ![]()
D.θ= ![]() ,t的最小值为
,t的最小值为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,函数g(x)=f(x)﹣k.
,函数g(x)=f(x)﹣k.
(1)当m=2时,若函数g(x)有两个零点,则k的取值范围是;
(2)若存在实数k使得函数g(x)有两个零点,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.
(I)求证:EM⊥AD;
(II)求二面角A﹣BE﹣C的余弦值;
(III)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为45°,若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an=logn(n+1)(n≥2,n∈N*).定义:使乘积a1·a2·a3……ak为正整数的k(k∈N*)叫做“和谐数”,则在区间[1,2018]内所有的“和谐数”的和为
A. 2036 B. 2048 C. 4083 D. 4096
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与点
与点![]() 的距离比它的直线
的距离比它的直线![]() 的距离小2.
的距离小2.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)![]() 是点
是点![]() 轨迹上互相垂直的两条弦,问:直线
轨迹上互相垂直的两条弦,问:直线![]() 是否经过
是否经过![]() 轴上一定点,若经过,求出该点坐标;若不经过,说明理由.
轴上一定点,若经过,求出该点坐标;若不经过,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com