
����Ŀ�����ŵ�������ķ�չ�����ǵĹ���ϰ�����ڸı䣬���������е�������ͨ�����繺������С����λ�������ˣ�ÿ�ι�����Ʒ�ɹ���Ե��̵���Ʒ�ͷ���������ۣ��ֶ�������200�γɹ�����������ͳ�ƣ�ͳ�ƽ�����±���ʾ��
�Է������ | �Է������� | �ϼ� | |
����Ʒ���� | 80 | 40 | 120 |
����Ʒ������ | 70 | 10 | 80 |
�ϼ� | 150 | 50 | 200 |
��1���Ƿ���![]() �İ�����Ϊ��Ʒ�������������й�? ��˵�����ɣ�
�İ�����Ϊ��Ʒ�������������й�? ��˵�����ɣ�
��2���ִ���200�ν����У�����������Ʒ��������������Ʒ�����������÷ֲ����ȡ��5�ν��ף�Ȼ�����5�ν�������ѡ���ν��й۲죬�������ν�����ǡ��һ��������Ʒ�������ĸ��ʣ�
���� (����
(����![]() ��
��
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���𰸡���1����![]() �İ�����Ϊ��Ʒ�������������й�.��������2��
�İ�����Ϊ��Ʒ�������������й�.��������2��![]()
��������
(1) ���ݱ������ݣ����� �����
�����![]() ��Ȼ�����ٽ�������½���.
��Ȼ�����ٽ�������½���.
(2) ���ݱ���õ�������Ʒ�ĺ�������Ƶ��Ϊ![]() ���õ����״���Ϊ3�Σ� ������Ĵ���Ϊ2�Σ�����һ���ŵ���ͣ��ȵõ���5�ν���������ȡ��2�εĻ����¼����������ҳ�ֻ��һ�κ����Ļ����¼��������빫ʽ���.
���õ����״���Ϊ3�Σ� ������Ĵ���Ϊ2�Σ�����һ���ŵ���ͣ��ȵõ���5�ν���������ȡ��2�εĻ����¼����������ҳ�ֻ��һ�κ����Ļ����¼��������빫ʽ���.
(1) ![]() ��
��
������![]() �İ�����Ϊ��Ʒ�������������й�.
�İ�����Ϊ��Ʒ�������������й�.
(2) �ɱ����֪������Ʒ�ĺ�������Ƶ��Ϊ![]() �����÷ֲ�����ķ�ʽ����200�ν�����ȡ��5�ν��ף�������Ľ��״���Ϊ3�Σ� ������Ĵ���Ϊ2��.
�����÷ֲ�����ķ�ʽ����200�ν�����ȡ��5�ν��ף�������Ľ��״���Ϊ3�Σ� ������Ĵ���Ϊ2��.
������Ľ���Ϊ![]() �� ������Ľ���
�� ������Ľ���![]() ��
��
��5�ν���������ȡ��2�ε�����ȡ��Ϊ![]() ��
��![]()
![]() ��
�� ![]() ��
�� ![]() �� ����10�������
�� ����10�������
����ֻ��һ�κ����������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �� ����6�����.
�� ����6�����.
��ˣ� ǡ��һ�κ����ĸ���Ϊ![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() ��
��![]() ��
��![]() �ı���ͬ����ָ���λͬѧ��ÿ�����ٷֵ�һ����ÿ���鶼�������˷ֵ���
�ı���ͬ����ָ���λͬѧ��ÿ�����ٷֵ�һ����ÿ���鶼�������˷ֵ���![]() ��
��![]() ����ͬʱ�ָ�ͬһ���ˣ���ͬ�ķ��䷽ʽ����__________�֣����������𣩣�
����ͬʱ�ָ�ͬһ���ˣ���ͬ�ķ��䷽ʽ����__________�֣����������𣩣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���о�ij��ϸ���ķ�ֳ����y������x�ı仯������ռ��������£�
����x | 1 | 2 | 3 | 4 | 5 | 6 |
��ֳ����y | 6 | 12 | 25 | 49 | 95 | 190 |
��1������ɢ��ͼ���ж�![]() ��
��![]() ��һ���ʺ���Ϊy����x�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
��һ���ʺ���Ϊy����x�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
��2�����ݣ�1���е��жϼ��������ݣ���y����x�Ļع鷽��![]() �ο����ݣ�
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
�ο���ʽ��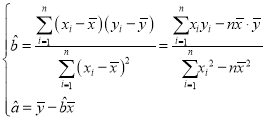
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ�������߸���ͬ�ĵ㣬����������һ��Ϊʼ�㣬��һ��Ϊ�յ����������������е����������ڵ�![]() ��
��![]() ������������
������������![]() ������������
������������![]() ��.������ij�ĵ���ȷ�����ı��ε�����������β��ӵ��ĸ������������Ϊ�����ı��Ρ�.���������߸������ĸ���Ϊ������ı����У����ı��θ��������ֵ
��.������ij�ĵ���ȷ�����ı��ε�����������β��ӵ��ĸ������������Ϊ�����ı��Ρ�.���������߸������ĸ���Ϊ������ı����У����ı��θ��������ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������![]() �ĵ�����
�ĵ�����![]() ��ͼ����ͼ��ʾ�������¹��ں���
��ͼ����ͼ��ʾ�������¹��ں���![]() ���жϣ�
���жϣ�
��������![]() �ڵ���������
�ڵ���������
��������![]() �ڵ����ݼ���
�ڵ����ݼ���
��������![]() �ڵ���������
�ڵ���������
��![]() �Ǽ�Сֵ�㣻
�Ǽ�Сֵ�㣻
��![]() �Ǽ���ֵ��.
�Ǽ���ֵ��.
������ȷ���ǣ� ��
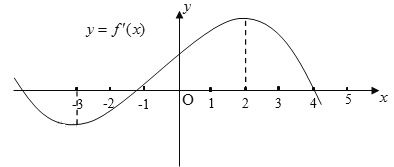
A. �ۢ�B. �ڢ�C. �٢ܢ�D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���о�����ѧ��ʽ���Խ�ѧ������Ӱ�죬ij������ѧ��ʦ�ֱ������ֲ�ͬ�Ľ�ѧ��ʽ����ѧ��ѧƽ�������������ʶ���ͬ�ļס���������һ�°���н�ѧ���ڷ̶ܳȺ��Ծ��Զ�һ����.���¾�ҶͼΪ�ס������ࣨÿ���Ϊ20�ˣ�ѧ������ѧ��ĩ���Գɼ���
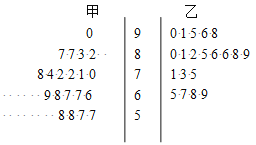
��1��ѧУ�涨���ɼ�������75�ֵ�Ϊ���㣮�����������![]() ��������
��������
�װ� | �Ұ� | �ϼ� | |
���� | |||
������ | |||
�ϼ� |
��2���ж��ж�������Ϊ���ɼ��������ѧ��ʽ�йء���
�����ٽ�ֵ�������ο���
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�ο���ʽ�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��������
��������![]() �ķ���
�ķ���![]() ǡ����������ȵ�ʵ������ ��ʵ��
ǡ����������ȵ�ʵ������ ��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]()
![]()
A. ![]() B.
B. ![]() ��
��![]() C.
C. ![]() ��
��![]() D.
D. ![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B����Ʒ�Ƹ����ֳ���2017��7�µ���������(��2017��6�±Ƚ�)���������±���
AƷ�Ƴ��� | A1 | A2 | A3 | ||||
���������� | -7.29% | 10.47% | 14.70% | ||||
BƷ�Ƴ��� | B1 | B2 | B3 | ||||
���������� | -8.49% | -28.06% | 13.25% | ||||
���ݴ˱��е����ݣ������¹���7�·��������ĸ�����:��A1����������B1���������ࣻ
��AƷ�����ֳ������������������ʿ��ܴ���14.70%��
��BƷ����������������������ʿ���Ϊ����
��AƷ�����ֳ������������������ʿ���С��BƷ�����ֳ������������������ʣ�
������ȷ���۵ĸ�����( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A={x|x2��9}��B={x|��1��x��7}��C={x||x��2|��4}��
��1����A��B��A��C��
��2����U=R����![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com