
【题目】某学校社团为调查学生课余学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图如图所示,将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

根据已知条件完成下面的![]() 列联表,并据此资料判断能不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关?
列联表,并据此资料判断能不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关?
非围棋迷 | 围棋迷 | 总计 | |
男 | |||
女 | 10 | 55 | |
总计 |
附: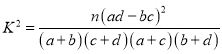 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行篮球决赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主”.设甲队主场取胜的概率为![]() ,客场取胜的概率为
,客场取胜的概率为![]() ,且各场比赛结果相互独立,则甲队不超过
,且各场比赛结果相互独立,则甲队不超过![]() 场即获胜的概率是( )
场即获胜的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,某地援鄂医护人员
日,某地援鄂医护人员![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 人(其中
人(其中![]() 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这
是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这![]() 名医护人员和接见他们的一位领导共
名医护人员和接见他们的一位领导共![]() 人站一排进行拍照,则领导和队长站在两端且
人站一排进行拍照,则领导和队长站在两端且![]() 相邻,而
相邻,而![]() 不相邻的排法种数为( )
不相邻的排法种数为( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了改善市民的生活环境,信阳市决定对信阳市的1万家中小型化工企业进行污染情况摸排,并出台相应的整治措施.通过对这些企业的排污口水质,周边空气质量等的检验,把污染情况综合折算成标准分100分,发现信阳市的这些化工企业污染情况标准分基本服从正态分布N(50,162),分值越低,说明污染越严重;如果分值在[50,60]内,可以认为该企业治污水平基本达标.
(1)如图是信阳市的某工业区所有被调查的化工企业的污染情况标准分的频率分布直方图,请计算这个工业区被调查的化工企业的污染情况标准分的平均值,并判断该工业区的化工企业的治污平均值水平是否基本达标;
(2)大量调査表明,如果污染企业继续生产,那么标准分低于18分的化工企业每月对周边造成的直接损失约为10万元,标准分在[18,34)内的化工企业每月对周边造成的直接损失约为4万元.长沙市决定关停80%的标准分低于18分的化工企业和60%的标准分在[18,34)内的化工企业,每月可减少的直接损失约有多少?
(附:若随机变量![]() ,则
,则![]() ,
, ![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,下图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每卦有三根线组成(“![]() ”表示一根阳线,“
”表示一根阳线,“![]() ”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率__________.
”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体![]() 中,M是线段AB上的动点.
中,M是线段AB上的动点.
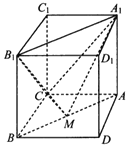
![]() 证明:
证明:![]() 平面
平面![]() ;
;
![]() 若点M是AB中点,求二面角
若点M是AB中点,求二面角![]() 的余弦值;
的余弦值;
![]() 判断点M到平面
判断点M到平面![]() 的距离是否为定值?若是,求出定值;若不是,请说明理由.
的距离是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com