
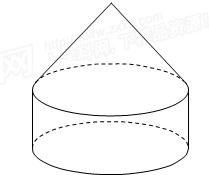
 要制作一个由同底圆锥和圆柱组成的储油罐(如图),设计要求:圆锥和圆柱的总高度和圆柱底面半径相等,都为r米.市场上,圆柱侧面用料单价为每平方米a元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为θ(弧度),总费用为y(元).
要制作一个由同底圆锥和圆柱组成的储油罐(如图),设计要求:圆锥和圆柱的总高度和圆柱底面半径相等,都为r米.市场上,圆柱侧面用料单价为每平方米a元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为θ(弧度),总费用为y(元).| h1 |
| r |
| 2 |
| cosθ |
| 2 |
| cosθ |
| 2sinθ-1 |
| cos2θ |
| π |
| 6 |
| 2sinθ-1 |
| cos2θ |
| h1 |
| r |
| π |
| 4 |
| 2r |
| cosθ |
| 2r |
| cosθ |
| 2 |
| cosθ |
| 2 |
| cosθ |
| π |
| 4 |
| 2sinθ-1 |
| cos2θ |
| π |
| 6 |
| 2sinθ-1 |
| cos2θ |
| π |
| 6 |
| 2sinθ-1 |
| cos2θ |
| π |
| 6 |
| π |
| 4 |
| 2sinθ-1 |
| cos2θ |
| π |
| 6 |
| π |
| 6 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 要制作一个由同底圆锥和圆柱组成的储油罐(如图),设计要求:圆锥和圆柱的总高度和圆柱底面半径相等,都为r米.市场上,圆柱侧面用料单价为每平方米a元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为θ(弧度),总费用为y(元).
要制作一个由同底圆锥和圆柱组成的储油罐(如图),设计要求:圆锥和圆柱的总高度和圆柱底面半径相等,都为r米.市场上,圆柱侧面用料单价为每平方米a元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为θ(弧度),总费用为y(元).查看答案和解析>>
科目:高中数学 来源:2010年江苏省镇江市高考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年江苏省镇江市高三第一次调研数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com