
【题目】以下5条表述中,横线上填A代表“充分非必要条件”,填B代表“必要非充分条件”,填C代表“充要条件”,填D代表“既非充分也非必要条件”,请将相应的字母填入下列横线上.
(1)若![]() ,则“
,则“![]() 是
是![]() 与
与![]() 的等比中项”是“
的等比中项”是“![]() ”的_______.
”的_______.
(2)“数列![]() 为常数列”是“数列
为常数列”是“数列![]() 既是等差数列又是等比数列”的_______.
既是等差数列又是等比数列”的_______.
(3)若![]() 是等比数列,则“
是等比数列,则“![]() ”是“
”是“![]() 为递减数列”的_______.
为递减数列”的_______.
(4)若![]() 是公比为
是公比为![]() 的等比数列,则“
的等比数列,则“![]() ”是“
”是“![]() 是递减数列”的_______.
是递减数列”的_______.
(5)记数列![]() 的前
的前![]() 项和为
项和为![]() ,则“数列
,则“数列![]() 为递增数列”是“数列
为递增数列”是“数列![]() 的各项均为大于零”的_______.
的各项均为大于零”的_______.
【答案】A B C D B
【解析】
根据充分条件、必要条件一一判断即可.
解:对于(1),![]() ,若
,若![]() 是
是![]() 与
与![]() 的等比中项则可得
的等比中项则可得![]() ,充分性成立,
,充分性成立,
若当![]() 时满足
时满足![]() 当时
当时![]() 不是
不是![]() 与
与![]() 的等比中项,故必要性不成立,即“
的等比中项,故必要性不成立,即“![]() 是
是![]() 与
与![]() 的等比中项”是“
的等比中项”是“![]() ”的充分不必要条件,故填
”的充分不必要条件,故填![]() ;
;
对于(2)若数列![]() 为常数列则数列
为常数列则数列![]() 是等差数列不一定是等比数列,如
是等差数列不一定是等比数列,如![]() 是各项均为
是各项均为![]() 的常数数列,故充分性不成立;
的常数数列,故充分性不成立;
若数列![]() 既是等差数列又是等比数列,则数列
既是等差数列又是等比数列,则数列![]() 一定为各项不为零的常数数列,故必要性成立;即“数列
一定为各项不为零的常数数列,故必要性成立;即“数列![]() 为常数列”是“数列
为常数列”是“数列![]() 既是等差数列又是等比数列”的必要不充分条件,故填
既是等差数列又是等比数列”的必要不充分条件,故填![]() ;
;
对于(3)已知数列![]() 是等比数,若
是等比数,若![]() 可得
可得![]() 为递减数列,故充分性成立;
为递减数列,故充分性成立;
若![]() 为递减数列,则必有
为递减数列,则必有![]() ,故必要性也成立,即“
,故必要性也成立,即“![]() ”是“
”是“![]() 为递减数列”的充要条件,故填
为递减数列”的充要条件,故填![]() ;
;
对于(4)![]() 是公比为
是公比为![]() 的等比数列,当
的等比数列,当![]() ,且
,且![]() 时,
时,![]() 是递减数列,或当
是递减数列,或当![]() ,且
,且![]() 时,
时,![]() 是递减数列,故“
是递减数列,故“![]() ”是“
”是“![]() 是递减数列”的既不充分也不必要条件,故填
是递减数列”的既不充分也不必要条件,故填![]() ;
;
对于(5)若数列![]() 为递增数列不能得到数列
为递增数列不能得到数列![]() 的各项均为大于零,故充分性不成立,若数列
的各项均为大于零,故充分性不成立,若数列![]() 的各项均为大于零则数列
的各项均为大于零则数列![]() 为递增数列,故必要性成立,即“数列
为递增数列,故必要性成立,即“数列![]() 为递增数列”是“数列
为递增数列”是“数列![]() 的各项均为大于零”的必要不充分条件,故填
的各项均为大于零”的必要不充分条件,故填![]() ;
;
故答案为:(1). A (2). B (3). C (4). D (5). B


科目:高中数学 来源: 题型:
【题目】某水产品经销商销售某种鲜鱼,售价为每千克![]() 元,成本为每千克
元,成本为每千克![]() 元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失
元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失![]() 元.根据以往的市场调查,将市场日需求量(单位:千克)按
元.根据以往的市场调查,将市场日需求量(单位:千克)按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到如图的频率分布直方图.
进行分组,得到如图的频率分布直方图.

(Ⅰ)未来连续三天内,连续两天该种鲜钱的日需求量不低于![]() 千克,而另一天的日需求量低于
千克,而另一天的日需求量低于![]() 千克的概率;
千克的概率;
(Ⅱ)在频率分布直方图的日需求量分组中,以各组区间的中点值代表该组的各个值,并以日需求量落入该区间的频率作为日需求量取该区间中点值的概率.若经销商每日进货![]() 千克,记经销商每日利润为
千克,记经销商每日利润为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点![]() (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点 |
D.若往容器内再注入 |
其中真命题的代号是: (写出所有真命题的代号).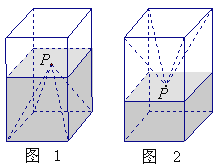
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上一点,
为抛物线上一点,![]() 为坐标原点,
为坐标原点,![]() 的外接圆与抛物线的准线相切,且外接圆的周长为
的外接圆与抛物线的准线相切,且外接圆的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,设不垂直于
,设不垂直于![]() 轴的直线
轴的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若
,若![]() ,证明直线
,证明直线![]() 过定点并写出定点坐标.
过定点并写出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面定义一个同学数学成绩优秀的标志为:“连续![]() 次考试成绩均不低于
次考试成绩均不低于![]() 分”.现有甲、乙、丙三位同学连续
分”.现有甲、乙、丙三位同学连续![]() 次数学考试成绩的记录数据(记录数据都是正整数):
次数学考试成绩的记录数据(记录数据都是正整数):
①甲同学:![]() 个数据的中位数为
个数据的中位数为![]() ,众数为
,众数为![]() ;
;
②乙同学:![]() 个数据的中位数为
个数据的中位数为![]() ,总体均值为
,总体均值为![]() ;
;
③丙同学:![]() 个数据的中位数为
个数据的中位数为![]() ,总体均值为
,总体均值为![]() ,总体方差为
,总体方差为![]() ;
;
则可以判定数学成绩优秀同学为()
A. 甲、丙B. 乙、丙C. 甲、乙D. 甲、乙、丙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() 点
点![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() (
(![]() 为实数).
为实数).

(1)求二面角![]() 的余弦值;
的余弦值;
(2)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(3)求证:直线![]() 与直线
与直线![]() 不可能垂直.
不可能垂直.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com