
【题目】如图,已知![]() 平面
平面![]() 平面
平面![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据条件可证四边形
,根据条件可证四边形![]() 为平行四边形,则
为平行四边形,则![]() ,再利用线面垂直的判定定理证明
,再利用线面垂直的判定定理证明![]() 平面
平面![]() ,最后根据面面垂直的判定定理证明结论即可;
,最后根据面面垂直的判定定理证明结论即可;
(2)在平面![]() 内,过点
内,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,利用线面角的定义找到直线与平面所成角
,利用线面角的定义找到直线与平面所成角![]() ,再通过解三角形得到
,再通过解三角形得到![]() 和
和![]() 即可求出结果.
即可求出结果.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 且
且![]() .
.
∵![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,
,
∴四边形![]() 为平行四边形,则
为平行四边形,则![]() .
.
∵![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,故
,故![]() 平面
平面![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
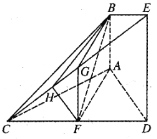
(2)在平面![]() 内,过点
内,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 为
为![]() 和平面
和平面![]() 所成的角,
所成的角,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,
∴直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【点晴】
本题考查面面垂直的证明、空间直线和平面的位置关系以及空间角的计算,考查考生的推理论证能力以及运算求解能力,属中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的右焦点F为抛物线
的右焦点F为抛物线![]() 的焦点,点M为
的焦点,点M为![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
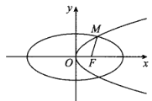
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,过焦点F的直线l与
,过焦点F的直线l与![]() 相交于A,B两点,已知
相交于A,B两点,已知![]() ,求
,求![]() 取得最大值时直线l的方程.
取得最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 分别是椭圆
分别是椭圆![]() :
:![]() (
(![]() )的左右焦点,点
)的左右焦点,点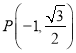 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .若椭圆
.若椭圆![]() 的内接四边形
的内接四边形![]() 的边
的边![]() 的延长线交于椭圆外一点
的延长线交于椭圆外一点![]() ,且点
,且点![]() 的横坐标为1,记直线
的横坐标为1,记直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
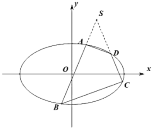
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为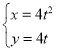 (其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线C2的极坐标方程为
(其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线C2的极坐标方程为![]() .
.
(1)把曲线C1的方程化为普通方程,C2的方程化为直角坐标方程;
(2)若曲线C1,C2相交于A,B两点,AB的中点为P,过点P做曲线C2的垂线交曲线C1于E,F两点,求|PE||PF|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2AD=4,过AA1作平面α使BD⊥α,且平面α∩平面A1B1C1D1=l,M∈l.下面给出了四个命题:这四个命题中,真命题的个数为( )
①l∥AC;
②BM⊥AC;
③l和AD1所成的角为60°;
④线段BM长度的最小值为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
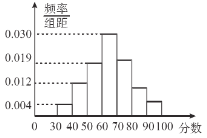
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)(ⅰ)若采用分层抽样的方法从分数落在区间![]() ,
,![]() 内抽取4人,求从分数落在区间
内抽取4人,求从分数落在区间![]() ,
,![]() 内各抽取的人数;
内各抽取的人数;
(ⅱ)从上述抽取的4人中再随机抽取2人,求这2人全部来自于区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备将1000万元资金投人到市环保工程建设中,现有甲,乙两个建设项目选择,若投资甲项目一年后可获得的利润![]() (万元)的概率分布列如表所示:
(万元)的概率分布列如表所示:
| 110 | 120 | 170 |
|
| 0.4 |
|
且![]() 的期望
的期望![]() ;若投资乙项目一年后可获得的利润
;若投资乙项目一年后可获得的利润![]() (万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为
(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为![]() 和
和![]() .若乙项目产品价格一年内调整次数
.若乙项目产品价格一年内调整次数![]() (次数)与
(次数)与![]() 的关系如表所示:
的关系如表所示:
| 0 | 1 | 2 |
| 41.2 | 117.6 | 204.0 |
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l过点![]() 且倾斜角为
且倾斜角为![]() .以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为
.以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]() ,l与C交于M,N两点.
,l与C交于M,N两点.
(1)求C的直角坐标方程和![]() 的取值范围;
的取值范围;
(2)求MN中点H的轨迹的参数方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com