解:(I)由意知函数f(x)的定义域是(0,+∞)
又
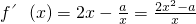
…(1分)
∴当a>0,由f(x)'>0可得
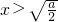
由

∴函数的单调递增区间为
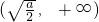
,
单调减区间为
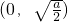
…(4分)
当a≤0时,f'(x)>0,∴函数的单调递增区间为(0,+∞)…(5分)
(II)当m=0时,函数F(x)的图象恒在x轴上方等价于F(x)>0在(1,+∞)上恒成立
由m=0,F(x)>0可得-alnx>-x∵x∈(1,+∞)
则

记
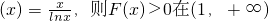
恒成立
等价于a<?(x)
min(x∈(1,+∞))
又
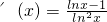
∴当x∈(1,e)时;?'(x)<0;当x∈(e,+∞)时,?'(x)>0
故?(x)在x=e处取得极小值,
也是最小值,即?(x)
min=?(e)=e∴a<e
故a的取值范围是(-∞,e).…(5分)
(III)函数F(x)在[1,3]上恰有两个不同的零点等价于方程x-2lnx=m,
在[1,3]上恰有两个相异实根.
令
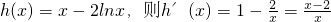
当x∈[1,2)时,h'(x)<0,当x∈(2,3]时,h'(x)>0
故在[1,3]上h(x)
min=h(2)=2-ln2…(8分)
又h(1)=1,h(3)=3-2ln3∵h(1)>h(3)∴只需h(2)<m≤h(3)
故m的取值范围是(2-2ln2,3-2ln3].…(9分)
分析:(I)先求函数的定义域,然后讨论a的正负,分别解不等式f(x)'>0与f(x)'<0,即可求出函数的单调区间;
(II)当m=0时,函数F(x)的图象恒在x轴上方等价于F(x)>0在(1,+∞)上恒成立,将a分离出来,然后研究另一侧函数的最小值即可求出a的范围;
(III)函数F(x)在[1,3]上恰有两个不同的零点等价于方程x-2lnx=m,在[1,3]上恰有两个相异实根,然后利用导数研究y=x-2lnx在[1,3]的值域即可求出m的范围.
点评:本题主要考查了利用导数研究函数的值域、研究闭区间上的值域等有关问题,是一道综合题,属于中档题.

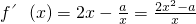 …(1分)
…(1分)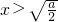

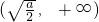 ,
,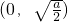 …(4分)
…(4分)
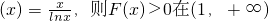 恒成立
恒成立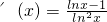
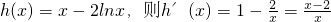


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案