
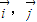 分别是x轴,y轴方向上的单位向量,
分别是x轴,y轴方向上的单位向量,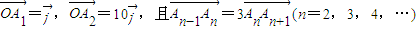 ,在射线y=x(x≥0)上从下到上依次有点Bi=(i=1,2,3,…),
,在射线y=x(x≥0)上从下到上依次有点Bi=(i=1,2,3,…),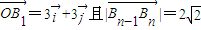 (n=2,3,4…).
(n=2,3,4…). ;
; ;
; ,
,
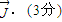

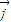 ,
,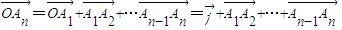
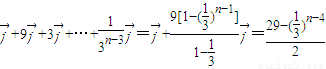

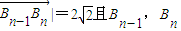 均在射线y=x(x≥0)上,
均在射线y=x(x≥0)上, =
=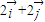 .∴
.∴
 =2n+3.
=2n+3. .
.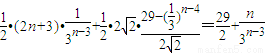 ,(10分)
,(10分) <0,
<0, (12分)
(12分)

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
| OP |
| e1 |
| e2 |
| e1 |
| e2 |
| 2 |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
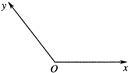 如图,在平面斜坐标系xOy中,∠xOy=135°.斜坐标定义:如果
如图,在平面斜坐标系xOy中,∠xOy=135°.斜坐标定义:如果| OP |
| 2 |
| OP |
| AP |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AP |
| ||
| 2 |
| PB |
| AB |
| 3 |
| KM |
| KN |
查看答案和解析>>
科目:高中数学 来源:河北省衡水中学2008-2009学年高三上学期期中考试(数学) 题型:044
已知![]() 分别是x轴、y轴方向上的单位向量,
分别是x轴、y轴方向上的单位向量,![]() ,且
,且![]() ,在射线y=x(x≥0)上从下到上依次有点Bi(i=1,2,3…),
,在射线y=x(x≥0)上从下到上依次有点Bi(i=1,2,3…),![]() 且
且![]()
(1)求![]() ;
;
(2)求![]() ;
;![]()
(3)求四边形AnAn+1Bn+1Bn面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com