
【题目】已知函数f(x)= ![]() ,直线y=
,直线y= ![]() x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣ ![]() }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
【答案】
(1)解:函数f(x)= ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() ,
,
设切点为(m,n),即有n= ![]() ,n=
,n= ![]() m,
m,
可得ame=em,①
由直线y= ![]() x为曲线y=f(x)的切线,可得
x为曲线y=f(x)的切线,可得
![]() =
= ![]() ,②
,②
由①②解得m=1,a=1;
(2)解:函数g(x)=min{f(x),x﹣ ![]() }(x>0),
}(x>0),
由f(x)= ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() ,
,
当0<x<2时,f(x)递增,x>2时,f(x)递减.
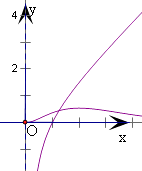
对x﹣ ![]() 在x>0递增,设y=f(x)和y=x﹣
在x>0递增,设y=f(x)和y=x﹣ ![]() 的交点为(x0,y0),
的交点为(x0,y0),
由f(1)﹣(1﹣1)= ![]() >0,f(2)﹣(2﹣
>0,f(2)﹣(2﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() <0,即有1<x0<2,
<0,即有1<x0<2,
当0<x<x0时,g(x)=x﹣ ![]() ,
,
h(x)=g(x)﹣cx2=x﹣ ![]() ﹣cx2,h′(x)=1+
﹣cx2,h′(x)=1+ ![]() ﹣2cx,
﹣2cx,
由题意可得h′(x)≥0在0<x<x0时恒成立,
即有2c≤ ![]() +
+ ![]() ,由y=
,由y= ![]() +
+ ![]() 在(0,x0)递减,
在(0,x0)递减,
可得2c≤ ![]() +
+ ![]() ①
①
当x≥x0时,g(x)= ![]() ,
,
h(x)=g(x)﹣cx2= ![]() ﹣cx2,h′(x)=
﹣cx2,h′(x)= ![]() ﹣2cx,
﹣2cx,
由题意可得h′(x)≥0在x≥x0时恒成立,
即有2c≤ ![]() ,由y=
,由y= ![]() ,可得y′=
,可得y′= ![]() ,
,
可得函数y在(3,+∞)递增;在(x0,3)递减,
即有x=3处取得极小值,且为最小值﹣ ![]() .
.
可得2c≤﹣ ![]() ②,
②,
由①②可得2c≤﹣ ![]() ,解得c≤﹣
,解得c≤﹣ ![]() .
.
【解析】(1)求出f(x)的导数,设出切点(m,n),可得切线的斜率,由切线方程可得a,m的方程,解方程可得a=1;(2)y=f(x)和y=x﹣ ![]() 的交点为(x0 , y0),分别画出y=f(x)和y=x﹣
的交点为(x0 , y0),分别画出y=f(x)和y=x﹣ ![]() 在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.
在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥E-ABCD中,四边形ABCD是平行四边形,△BCE是等边三角形,△ABE是等腰直角三角形,∠BAE=90°,且AC=BC.

(1)证明:平面ABE⊥平面BCE;
(2)求二面角A-DE-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为万元. 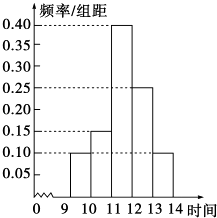
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,四点
,四点![]() 、
、![]() 、
、![]() 、
、![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上。
上。
(1)求![]() 的方程:
的方程:
(2)椭圆![]() 上是否存在不同的两点
上是否存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称?若存在,请求出直线
对称?若存在,请求出直线![]() 的方程,若不存在,请说明理由;
的方程,若不存在,请说明理由;
(3)设直线![]() 不经过点
不经过点![]() 且与
且与![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率的和为1,求证:
的斜率的和为1,求证:![]() 过定点。
过定点。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ,现建立以
,现建立以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系.
轴的正半轴为极轴的极坐标系.
(1)写出直线![]() 极坐标方程,曲线
极坐标方程,曲线![]() 的参数方程;
的参数方程;
(2)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(点
两点(点![]() 均在第一象限),且直线
均在第一象限),且直线![]() 的斜率成等比数列,证明:直线
的斜率成等比数列,证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏. 
(1)若当∠OBC= ![]() 时,sin∠BCO=
时,sin∠BCO= ![]() ,求此时a的值;
,求此时a的值;
(2)设y=CA2+CB2 , 且CA2+CB2≤232.
(i)试将y表示为a的函数,并求出a的取值范围;
(ii)若同时要求市民在水池边缘任意一点C处观赏喷泉时,观赏角度∠ACB的最大值不小于 ![]() ,试求A,B两处喷泉间距离的最小值.
,试求A,B两处喷泉间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( ) 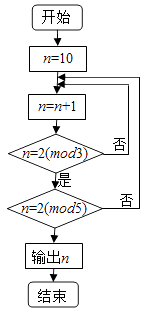
A.17
B.16
C.15
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,a,b,c分别为内角A,B,C的对边,2asin A=(2b+c)sin B+(2c+b)sin C.
且sin B+sin C=1,则△ABC是( )
A. 等腰钝角三角形 B. 等腰直角三角形 C. 钝角三角形 D. 直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com