
【题目】一次数学知识竞赛中,两组学生成绩如下表:
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
已经算得两个组的平均分都是80分,请根据你所学过的统计知识,进一步判断这两个组这次竞赛中成绩谁优谁次,并说明理由.
【答案】见解析
【解析】
试题根据题目所提供的甲组和乙组的竞赛成绩,用我们所学过的统计知识进行分析对比判断两组这次竞赛成绩,首先平均分一致,平均实力相当,其一看众数甲组好于乙组,其二看方差甲组较小,说明甲组成绩较稳定,其三看中位数甲组在中位数以上的人数比乙组在中位数以上的人数多,说明甲组总体成绩较好,其四高分段人数和满分人数乙组人数较多,乙组好于甲组,从不同角度利用统计量数据的考查可以得出相应的判断.
试题解析:
(1)甲组成绩的众数为90分,乙组成绩的众数为70分,从成绩的众数比较看,甲组成绩好些.
(2)![]() ×[2×(50-80)2+5×(60-80)2+10×(70-80)2+13×(80-80)2+14×(90-80)2+6×(100-80)2]=
×[2×(50-80)2+5×(60-80)2+10×(70-80)2+13×(80-80)2+14×(90-80)2+6×(100-80)2]=![]() ×(2×900+5×400+10×100+13×0+14×100+6×400)=172.
×(2×900+5×400+10×100+13×0+14×100+6×400)=172.
![]() =
=![]() ×(4×900+4×400+16×100+2×0+12×100+12×400)=256.
×(4×900+4×400+16×100+2×0+12×100+12×400)=256.
因为![]() ,所以甲组成绩较乙组成绩稳定.
,所以甲组成绩较乙组成绩稳定.
(3)甲、乙两组成绩的中位数、平均数都是80分,其中甲组成绩在80分以上(含80分)的有33人,乙组成绩在80分以上(含80分)的有26人,从这一角度看,甲组成绩总体较好.
(4)从成绩统计表看,甲组成绩大于或等于90分的人数为20人,乙组成绩大于或等于90分的人数为24人,所以乙组成绩在高分阶段的人数多,同时,乙组得满分的比甲组得满分的多6人,从这一角度看,乙组成绩较好.


科目:高中数学 来源: 题型:
【题目】在等腰![]() 中,
中, ![]() ,腰长为
,腰长为![]() ,
, ![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折,得到四棱锥
翻折,得到四棱锥![]() ,且
,且![]() 为棱
为棱![]() 中点,
中点, ![]() .
.
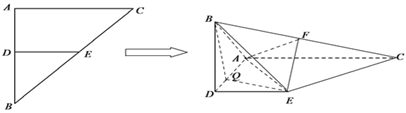
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求二面角
?若存在,求二面角![]() 的余弦值,若不存在,请说明理由.
的余弦值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下结论错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.命题“![]() ”是“
”是“![]() ”的充分条件
”的充分条件
C.命题“若![]() ,则
,则![]() 有实根”的逆命题为真命题
有实根”的逆命题为真命题
D.命题“![]() ,则
,则![]() 或
或![]() ”的否命题是“
”的否命题是“![]() ,则
,则![]() 且
且![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速(单位: ![]() ),现将其分成六组为
),现将其分成六组为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
(1)某小型轿车途经该路段,其速度在![]() 以上的概率是多少?
以上的概率是多少?
(2)若对车速在![]() ,
, ![]() 两组内进一步抽测两辆小型轿车,求至少有一辆小型轿车速度在
两组内进一步抽测两辆小型轿车,求至少有一辆小型轿车速度在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为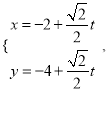 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com