
【题目】集合A={x|3≤x<9},B={x|1<x<7},C={x|x>m}.
(1)求A∪B;
(2)求(RA)∩B;
(3)若BC,求实数m的取值范围.
【答案】
(1)解: A={x|3≤x<9},B={x|1<x<7},
∴A∪B={x|1<x<9};
(2)解:RA={x|x<3或x≥9},
(RA)∩B={x|1<x<3};
(3)解:∵B={x|1<x<7},C={x|x>m},
且BC,
∴m≤1
【解析】(1)根据并集的定义求出A∪B即可;(2)根据补集和交集的定义进行计算即可;(3)利用子集的定义,即可求出m的取值范围.
【考点精析】掌握集合的并集运算和交、并、补集的混合运算是解答本题的根本,需要知道并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立;求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.
B,反之也成立;求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.


科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人每人有一张游泳比赛的门票,已知每张票可以观看指定的三场比赛中的任一场(三场比赛时间不冲突),甲乙二人约定他们会观看同一场比赛并且他俩观看每场比赛的可能性相同,又已知丙观看每一场比赛的可能性也相同,且甲乙的选择与丙的选择互不影响.
(1)求三人观看同一场比赛的概率;
(2)记观看第一场比赛的人数是![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:BD的长为 . 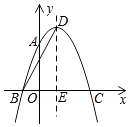
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x. 
(1)现已画出函数f(x)在y轴左侧的图像,如图所示,请补出完整函数f(x)的图像,并根据图像写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样统计,先将800人按001,002,003,…,800进行编号.
(Ⅰ)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号:(下面摘取了第7行至第9行)

(Ⅱ)抽的100人的数学与地理的水平测试成绩如下表:

成绩优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率为30%,求![]() 的值.
的值.
(Ⅲ)将![]() ,
, ![]() 的
的![]() 表示成有序数对
表示成有序数对![]() ,求“地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对
,求“地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log ![]() (x2﹣ax+b). (Ⅰ)若函数f(x)的定义域为(﹣∞,2)∪(3,+∞),求实数a,b的值;
(x2﹣ax+b). (Ⅰ)若函数f(x)的定义域为(﹣∞,2)∪(3,+∞),求实数a,b的值;
(Ⅱ)若f(﹣2)=﹣3且f(x)在(﹣∞,﹣1]上为增函数,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2ax+b , 且f(1)= ![]() 、f(2)=
、f(2)= ![]() .
.
(1)求a、b的值;
(2)判断f(x)的奇偶性并证明;
(3)先判断并证明函数f(x)在[0,+∞)上的单调性,然后求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
, ![]() 交
交![]() 于点
于点![]() .现将
.现将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,得到图2.
,得到图2.
(Ⅰ)在图2中,求证: ![]() ;
;
(Ⅱ)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在什么位置时,二面角
在什么位置时,二面角![]() 的余弦值为
的余弦值为![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校选择高一年级三个班进行为期二年的教学改革试验,为此需要为这三个班各购买某种设备1台.经市场调研,该种设备有甲乙两型产品,甲型价格是3000元/台,乙型价格是2000元/台,这两型产品使用寿命都至少是一年,甲型产品使用寿命低于2年的概率是![]() ,乙型产品使用寿命低于2年的概率是
,乙型产品使用寿命低于2年的概率是![]() .若某班设备在试验期内使用寿命到期,则需要再购买乙型产品更换.
.若某班设备在试验期内使用寿命到期,则需要再购买乙型产品更换.
(1)若该校购买甲型2台,乙型1台,求试验期内购买该种设备总费用恰好是10000元的概率;
(2)该校有购买该种设备的两种方案, ![]() 方案:购买甲型3台;
方案:购买甲型3台; ![]() 方案:购买甲型2台乙型1台.若根据2年试验期内购买该设备总费用的期望值决定选择哪种方案,你认为该校应该选择哪种方案?
方案:购买甲型2台乙型1台.若根据2年试验期内购买该设备总费用的期望值决定选择哪种方案,你认为该校应该选择哪种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com