练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

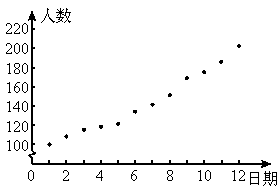
    2003年春季，我国部分地区SARS流行，党和政府采取果断措施，防治结合，很快使病情得到控制．下表是某同学记载的5月1日至5月12日每天北京市SARS治愈者数据，及根据这些数据绘制出的散点图(如图)．

    下列说法：

    ①根据此散点图，可以判断日期与人数具有线性相关关系．

    ②根据此散点图，可以判断日期与人数具有一次函数关系．

    其中正确的个数为

    [　　]

    A．0
    B．1
    C．2
    D．以上都不对
    答案：B
    提示：

    ①正确．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    2003年春季，我国部分地区SARS流行，党和政府采取果断措施，防治结合，很快使病情得到控制，下表是某同学记载的5月1日至5月12日每天北京市SARS治愈者数据，以及根据这些数据绘制出的散点图
    日期 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 5.10 5.11 5.12
    人数 100 109 115 118 121 134 141 152 168 175 186 203
    下列说法：
    ①根据此散点图，可以判断日期与人数具有线性相关关系；
    ②根据此散点图，可以判断日期与人数具有一次函数关系．
    其中正确的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    2003年春季，我国部分地区SARS流行，党和政府采取果断措施，防治结合，很快使病情得到控制．下表是某同学记载的5月1日至5月12日每天北京市SARS治愈者数据，及根据这些数据绘制出的散点图(如图)．

    下列说法：

    ①根据此散点图，可以判断日期与人数具有线性相关关系．

    ②根据此散点图，可以判断日期与人数具有一次函数关系．

    其中正确的个数为

    [　　]

    A．0

    B．1

    C．2

    D．以上都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    2003年春季，我国部分地区SARS流行，党和政府采取果断措施，防治结合，很快使病情得到控制，下表是某同学记载的5月1日至5月12日每天北京市SARS病患治愈者数据：

    根据这些数据绘制出散点图：

    判断日期与治愈人数是否具有相关关系？若有，具有怎样的相关关系？

    查看答案和解析>>

    科目：高中数学 来源：《2.3.1 变量之间的相关关系-2.3.2 两个变量的线性相关》2013年同步练习（解析版） 题型：选择题

    2003年春季，我国部分地区SARS流行，党和政府采取果断措施，防治结合，很快使病情得到控制，下表是某同学记载的5月1日至5月12日每天北京市SARS治愈者数据，以及根据这些数据绘制出的散点图
    日期5.15.25.35.45.55.65.75.85.95.105.115.12
    人数100109115118121134141152168175186203
    下列说法：
    ①根据此散点图，可以判断日期与人数具有线性相关关系；
    ②根据此散点图，可以判断日期与人数具有一次函数关系．
    其中正确的个数为（ ）
    A．0个
    B．1个
    C．2个
    D．以上都不对

    查看答案和解析>>

    科目：高中数学 来源：0101 月考题 题型：单选题

    2003年春季，我国部分地区SARS流行，党和政府采取果断措施，防治结合，很快使病情得到控制。下表是某同学记载的5月1日至5月12日每天北京市SARS病患者治愈者数据及散点图，


    下列说法：
    ①根据此散点图，可以判断日期与人数具有线性相关关系；
    ②若日期与人数具有线性相关关系，则相关系数r与临界值r0.05应满足|r|＞r0.05；
    ③根据此散点图，可以判断日期与人数具有一次函数关系；
    其中正确的个数为

    [     ]

    A．0个
    B．1个
    C．2个
    D．3个

    查看答案和解析>>

    同步练习册答案