
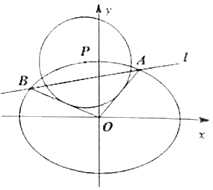
 如图,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,P为椭圆E上的动点,P到点M(0,2)的距离的最大值为$\frac{2}{3}\sqrt{21}$,直线l交椭圆于A(x1,y1)、B(x2,y2)两点.
如图,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,P为椭圆E上的动点,P到点M(0,2)的距离的最大值为$\frac{2}{3}\sqrt{21}$,直线l交椭圆于A(x1,y1)、B(x2,y2)两点.分析 (1)$\frac{c}{a}=\frac{\sqrt{3}}{2}$,a2=b2+c2,可得a=2b,$c=\sqrt{3}b$.可得椭圆的标准方程为:$\frac{{x}^{2}}{4}$+y2=b2.设P(x,y),(-b≤y≤b).P到点M(0,2)的距离d=$\sqrt{{x}^{2}+(y-2)^{2}}$=$\sqrt{4{b}^{2}+\frac{16}{3}-3(y+\frac{2}{3})^{2}}$.当0<b<$\frac{2}{3}$时,y=-b时,d取得最大值,舍去.
当$\frac{2}{3}$≤b时,y=-$\frac{2}{3}$时,d取得最大值,可得$\sqrt{4{b}^{2}+\frac{16}{3}}$=$\frac{2}{3}\sqrt{21}$,解得b即可得出.
(2)(i)设P(m,n),则$\frac{{m}^{2}}{4}+{n}^{2}$=1.⊙P的方程为:(x-m)2+(y-n)2=$\frac{4}{5}$,设经过原点O的⊙P的切线方程为:y=kx,不妨设OA的方程为:y=k1x,OB的方程为:y=k2x.则$\frac{|km-n|}{\sqrt{1+{k}^{2}}}$=$\frac{2\sqrt{5}}{5}$,化为:(5m2-4)k2-10mnk+5n2-4=0,联立$\left\{\begin{array}{l}{y={k}_{1}x}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,解得x1,y1.同理可得:x2,y2.假设存在常数λ,使x1x2+λy1y2=0恒成立,代入即可得出.
(ii)由(i)可得:OA⊥OB,|OA|2=${x}_{1}^{2}+{y}_{1}^{2}$=4,|OA|=2,同理可得:|OB|=2.即可得出S△OAB=$\frac{1}{2}|OA|•|OB|$.
解答 解:(1)∵$\frac{c}{a}=\frac{\sqrt{3}}{2}$,a2=b2+c2,可得a=2b,$c=\sqrt{3}b$.
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}$+y2=b2,
设P(x,y),(-b≤y≤b).
P到点M(0,2)的距离d=$\sqrt{{x}^{2}+(y-2)^{2}}$=$\sqrt{4({b}^{2}-{y}^{2})+({y}^{2}-4y+4)}$=$\sqrt{4{b}^{2}+\frac{16}{3}-3(y+\frac{2}{3})^{2}}$,
当0<b<$\frac{2}{3}$时,y=-b时,d取得最大值,∴b+2=$\frac{2}{3}\sqrt{21}$,解得b=$\frac{2}{3}\sqrt{21}$-2$>\frac{2}{3}$,舍去.
当$\frac{2}{3}$≤b时,y=-$\frac{2}{3}$时,d取得最大值,∴$\sqrt{4{b}^{2}+\frac{16}{3}}$=$\frac{2}{3}\sqrt{21}$,解得b=1,满足条件.
∴椭圆E的方程为:$\frac{{x}^{2}}{4}$+y2=1.
(2)(i)设P(m,n),则$\frac{{m}^{2}}{4}+{n}^{2}$=1.
⊙P的方程为:(x-m)2+(y-n)2=$\frac{4}{5}$,
设经过原点O的⊙P的切线方程为:y=kx,不妨设OA的方程为:y=k1x,OB的方程为:y=k2x.
则$\frac{|km-n|}{\sqrt{1+{k}^{2}}}$=$\frac{2\sqrt{5}}{5}$,化为:(5m2-4)k2-10mnk+5n2-4=0,
∴k1+k2=$\frac{10mn}{5{m}^{2}-4}$,k1k2=$\frac{5{n}^{2}-4}{5{m}^{2}-4}$,
联立$\left\{\begin{array}{l}{y={k}_{1}x}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,解得x1=$\frac{2}{\sqrt{1+{k}_{1}^{2}}}$,y1=$\frac{2{k}_{1}}{\sqrt{1+{k}_{1}^{2}}}$.
同理可得:${x}_{2}=\frac{-2}{\sqrt{1+{k}_{2}^{2}}}$,y2=$\frac{-2{k}_{2}}{\sqrt{1+{k}_{2}^{2}}}$.
假设存在常数λ,使x1x2+λy1y2=0恒成立,则$\frac{-4}{\sqrt{(1+{k}_{1}^{2})(1+{k}_{2}^{2})}}$+$\frac{-4λ{k}_{1}{k}_{2}}{\sqrt{(1+{k}_{1}^{2})(1+{k}_{2}^{2})}}$=0,
解得λ=-k1k2=-$\frac{5{n}^{2}-4}{5{m}^{2}-4}$=-$\frac{5(1-\frac{{m}^{2}}{4})-4}{5{m}^{2}-4}$=$\frac{1}{4}$为常数.
(ii)由(i)可得:OA⊥OB,|OA|2=${x}_{1}^{2}+{y}_{1}^{2}$=$\frac{4}{1+{k}_{1}^{2}}+\frac{4{k}_{1}^{2}}{1+{k}_{1}^{2}}$=4,∴|OA|=2,
同理可得:|OB|=2.
∴S△OAB=$\frac{1}{2}|OA|•|OB|$=2.
点评 本题考查了椭圆的定义及其标准方程、直线与椭圆相交问题、直线与圆相切性质、一元二次方程的根与系数的关系、点到直线的距离公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(0,+∞) | B. | (-∞,0)∪(2,+∞) | C. | (2,3) | D. | (-2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3 | C. | $\frac{5}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com