
【题目】某同学用“五点法”画函数 ![]() 在区间[﹣
在区间[﹣ ![]() ,
, ![]() ]上的图象时,列表并填入了部分数据,如表:
]上的图象时,列表并填入了部分数据,如表:
2x﹣ | ﹣ | ﹣π | ﹣ | 0 |
|
|
x | ﹣ | ﹣ | ﹣ |
|
|
|
f(x) |
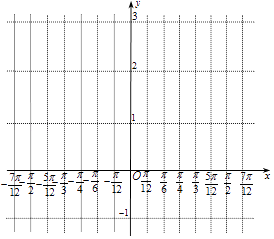
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出f(x)在区间[﹣ ![]() ,
, ![]() ]上的图象;
]上的图象;
(2)求f(x)的最小值及取最小值时x的集合;
(3)求f(x)在 ![]() 时的值域.
时的值域.
【答案】
(1)解:数据补全如下表:
2x﹣ | ﹣ | ﹣π | ﹣ | 0 |
|
|
x | ﹣ | ﹣ | ﹣ |
|
|
|
f(x) |
| 1 | ﹣1 | 1 | 3 |
|
故f(x)在区间[﹣ ![]() ,
, ![]() ]上的图象如图所示.
]上的图象如图所示.

(2)解:当 ![]() ,
,
即 ![]() 时,f(x)取最小值﹣1.
时,f(x)取最小值﹣1.
取最小值时x的集合为 ![]()
(3)解:当 ![]() 时,
时, ![]() ,
,
故 ![]()
所以 ![]() ,即f(x)在
,即f(x)在 ![]() 时的值域为
时的值域为 ![]()
【解析】(1)先把数据补全,利用描点法能在给出的直角坐标系中,画出f(x)在区间[﹣ ![]() ,
, ![]() ]上的图象.(2)利用正弦函数的图象及性质能求出函数
]上的图象.(2)利用正弦函数的图象及性质能求出函数 ![]() 的最小值及取最小值时x的集合.(3)当
的最小值及取最小值时x的集合.(3)当 ![]() 时,
时, ![]() ,从而
,从而 ![]() ,由此能求出f(x)在
,由此能求出f(x)在 ![]() 时的值域.
时的值域.
【考点精析】掌握正弦函数的单调性和五点法作函数y=Asin(ωx+φ)的图象是解答本题的根本,需要知道正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).
上是减函数;描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=asin 2x+bcos 2x,其中a,b∈R,ab≠0.若f(x)≤|f( ![]() )|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ①
)|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ① ![]() ;②
;② ![]() ≥
≥ ![]() ;
;
③f(x)的单调递增区间是(kπ+ ![]() ,kπ+
,kπ+ ![]() )(k∈Z);
)(k∈Z);
④f(x)既不是奇函数也不是偶函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需把正弦曲线y=sinx上所有点( )
)的图象,只需把正弦曲线y=sinx上所有点( )
A.向右平移 ![]() 个单位长度,再将所得图象上的点横坐标缩短为原来的
个单位长度,再将所得图象上的点横坐标缩短为原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
B.向左平移 ![]() 个单位长度,再将所得图象上的点横坐标缩短为原来的
个单位长度,再将所得图象上的点横坐标缩短为原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
C.向右平移 ![]() 个单位长度,再将所得图象上的点横坐标伸长为原来的2倍,纵坐标不变
个单位长度,再将所得图象上的点横坐标伸长为原来的2倍,纵坐标不变
D.向左平移 ![]() 个单位长度,再将所得图象上的点横坐标缩短为原来的2倍,纵坐标不变
个单位长度,再将所得图象上的点横坐标缩短为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为得到函数y=cos(2x+ ![]() )的图象,只需将函数y=cos2x的图象( )
)的图象,只需将函数y=cos2x的图象( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有命题: ①y=|sinx﹣ ![]() |的周期是π;
|的周期是π;
②y=sinx+sin|x|的值域是[0,2];
③方程cosx=lgx有三解;
④ω为正实数,y=2sinωx在 ![]() 上递增,那么ω的取值范围是
上递增,那么ω的取值范围是 ![]() ;
;
⑤在y=3sin(2x+ ![]() )中,若f(x1)=f(x2)=0,则x1﹣x2必为π的整数倍;
)中,若f(x1)=f(x2)=0,则x1﹣x2必为π的整数倍;
⑥若A、B是锐角△ABC的两个内角,则点P(cosB﹣sinA,sinB﹣cosA在第二象限;
⑦在△ABC中,若 ![]() ,则△ABC钝角三角形.其中真命题个数为( )
,则△ABC钝角三角形.其中真命题个数为( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为零的等差数列,a1=1,且a2 , a4 , a8成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:a1b1+a2b2+a3b3+…+anbn=2n+1 , n∈N* , 令cn= ![]() ,n∈N* , 求数列{cncn+1}的前n项和Sn .
,n∈N* , 求数列{cncn+1}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)判断f(x)的奇偶性;
(2)判断f(x)在R上的单调性,并用定义证明;
(3)是否存在实数t,使不等式f(x﹣t)+f(x2﹣t2)≥0对一切x∈[1,2]恒成立?若存在,求出t的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com