
| x | 80 | 90 | 100 | 110 | 120 |
| y | 48 | 52 | 63 | 72 | 80 |
科目:高中数学 来源:不详 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
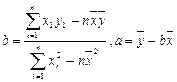 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 喜爱运动 | 不喜爱运动 | 总计 |
| 男 | 10 | | 16 |
| 女 | 6 | | 14 |
| 总计 | | | 30 |
 ,求
,求 的分布列和均值。
的分布列和均值。 ,其中
,其中
 | 0.40 | 0.25 | 0.10 | 0.010 |
 | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
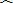 |
| y |
| |||||||
|
| |||||||
|
| . |
| y |
| . |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
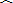 |
| y |
| A.y的值一定是0.5 | B.y的值一定不是O.5 |
| C.可以预测y的值0.5 | D.无法预测y的值 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| ? |
| y |
| A.y平均减少1.5个单位 | B.y平均减少2个单位 |
| C.y平均增加1.5个单位 | D.y平均增加2个单位 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 温度(x) | 0 | 10 | 20 | 30 | 40 |
| 溶解度(y) | 65 | 74 | 87 | 96 | 103 |
 |
| y |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
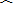 |
| y |
| A.在(-1,0)内 | B.在(-1,1)内 | C.在(0,1)内 | D.在[1,+∞)内 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(人) | 22 | 25 | 29 | 26 | 16 | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com