
如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN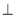 平面ABCD,E,F分别为MA,DC的中点,求证:
平面ABCD,E,F分别为MA,DC的中点,求证:
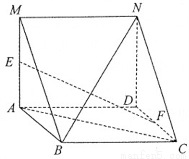
(1)EF//平面MNCB;
(2)平面MAC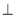 平面BND.
平面BND.
(1) (2)见解析
【解析】
试题分析:(1)取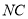 的中点
的中点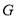 ,连接
,连接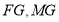 ,欲证
,欲证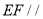 平面
平面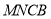 ,只要证
,只要证
只要证四边形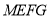 是平行四边形即可,事实上,由于
是平行四边形即可,事实上,由于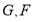 分别是
分别是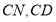 的中点,易知
的中点,易知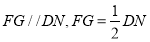 另一方面又有
另一方面又有 ,所以FG与ME平行且相等,四边形
,所以FG与ME平行且相等,四边形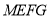 是平行四边形,问题得证.
是平行四边形,问题得证.
(2) 连接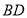 、
、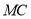 ,欲证
,欲证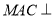 平面
平面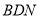 ,只要证
,只要证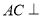 平面
平面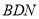 ,即证
,即证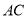 与平面
与平面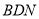 内的两条相交直线
内的两条相交直线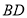 、
、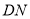 都垂直;由菱形
都垂直;由菱形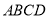 易知
易知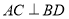 ;另外,由平面
;另外,由平面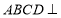 平面
平面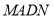
及矩形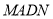 易证
易证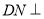 平面
平面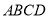 ,进而有
,进而有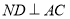 ,所以问题得证.
,所以问题得证.
试题解析:
证明:(1)取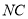 的中点
的中点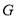 ,连接
,连接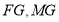 ,
,
因为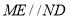 且
且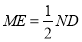 ,
,
又因为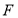 、
、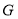 分别为
分别为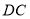 、
、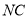 的中点,
的中点,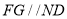 且
且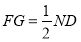 , 2分
, 2分
所以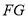 与
与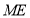 平行且相等,所以四边形
平行且相等,所以四边形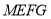 是平行四边形,
是平行四边形,
所以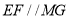 , 4分
, 4分
又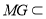 平面
平面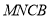 ,
,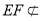 平面
平面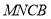 ,
,
所以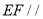 平面
平面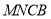 6分
6分
(2)连接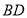 、
、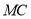 ,因为四边形
,因为四边形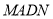 是矩形,
是矩形,
所以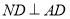 ,又因为平面
,又因为平面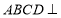 平面
平面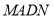
所以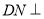 平面
平面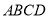 8分
8分
所以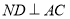
因为四边形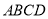 是菱形,所以
是菱形,所以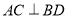
因为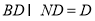 ,所以
,所以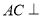 平面
平面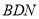 10分
10分
又因为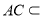 平面
平面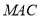
所以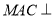 平面
平面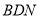 12分
12分
考点:1、直线与平面平行的判定;2、直线与平面及平面与平面垂直的判定与性质.


科目:高中数学 来源:2013-2014学年山东省潍坊市高三4月模拟考试文科数学试卷(解析版) 题型:选择题
为了调查学生携带手机的情况,学校对高一、高二、高三三个年级的学生进行分层抽样调查,已知高一有学生l000人、高二有1200人;三个年级总共抽取了66人,其中高一抽取了20人,则高三年级的全部学生数为( )
A.1000 B.1100 C.1200 D.1300
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试文科数学试卷(解析版) 题型:选择题
设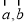 是两个非零向量,则下列命题为真命题的是
是两个非零向量,则下列命题为真命题的是
A.若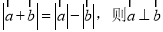
B.若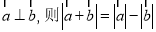
C.若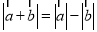 ,则存在实数
,则存在实数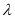 ,使得
,使得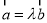
D.若存在实数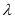 ,使得
,使得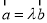 ,则
,则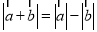
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试理科数学试卷(解析版) 题型:选择题
已知点M(x,y)是平面区域 内的动点,则
内的动点,则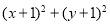 的最大值是( )
的最大值是( )
(A)10 (B)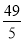 (C)
(C)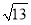 (D)13
(D)13
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试理科数学试卷(解析版) 题型:选择题
已知集合A={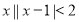 },B={
},B={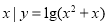 },设U=R,则A
},设U=R,则A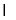 (
(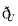 B)等于( )
B)等于( )
(A) [3,+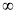 ) (B) (-1,0]
) (B) (-1,0]
(C) (3,+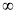 ) (D) [-1,0]
) (D) [-1,0]
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试文科数学试卷(解析版) 题型:选择题
已知直线m,n不重合,平面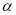 ,
,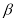 不重合,下列命题正确的是( )
不重合,下列命题正确的是( )
(A)若m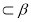 ,n
,n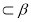 ,m//
,m//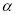 ,n//
,n//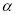 ,则
,则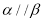
(B)若m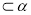 ,m
,m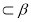 ,
,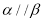 ,则m//n
,则m//n
(C)若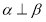 ,m
,m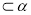 ,n
,n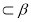 ,则
,则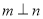
(D)若m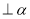 ,n
,n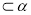 ,则
,则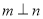
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三5月统一质量检测考试理科数学试卷(解析版) 题型:选择题
设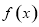 是定义在R上的偶函数,且
是定义在R上的偶函数,且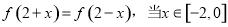 时,
时, ,若在区间
,若在区间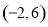 内,函数
内,函数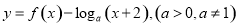 恰有1个零点,则实数
恰有1个零点,则实数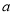 的取值范围是( )
的取值范围是( )
A. B.
B.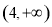 C.
C.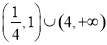 D.
D.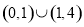
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com