
【题目】如图,在四棱锥![]() 中,
中,![]() 是边长为4的正三角形,
是边长为4的正三角形,![]() 且
且![]() ,
,![]() ,
,![]() ,
,![]() ,M为AB中点.
,M为AB中点.
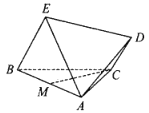
(Ⅰ)证明:![]() 平面ADE;
平面ADE;
(Ⅱ)求直线CA与平面BCDE所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)取AE的中点F,连接MF、FD,只需证明四边形MFDC为平行四边形,因为点M为AB的中点,所以![]() ,且
,且![]() ,则易证.
,则易证.
(Ⅱ)先证明![]() 平面ADE,作
平面ADE,作![]() 于
于![]() ,再证明
,再证明![]() 平面CDEB,所以
平面CDEB,所以![]() 为直线CA与平面BCDE所成的角,利用
为直线CA与平面BCDE所成的角,利用![]() ,求出
,求出![]() ,则直线CA与平面BCDE所成角的正弦值可求.
,则直线CA与平面BCDE所成角的正弦值可求.
(Ⅰ)证明:
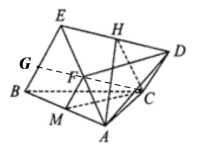
取AE的中点F,连接MF,FD,
因为点M为AB的中点,
所以![]() ,且
,且![]() ,
,
又因为![]() 且
且![]() ,
,
所以![]() ,
,![]() ,
,
所以四边形MFDC为平行四边形,所以![]() ,
,
又因为![]() 平面ADE,
平面ADE,![]() 平面ADE,
平面ADE,
所以![]() 平面ADE.
平面ADE.
(Ⅱ)解:因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,
,
所以![]() 平面ADE,
平面ADE,
又![]() 平面CDEB,
平面CDEB,
所以平面![]() 平面CDEB,
平面CDEB,
作![]() 于
于![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
,
所以![]() 平面CDEB,连接CH,
平面CDEB,连接CH,
所以![]() 为直线CA与平面BCDE所成的角.
为直线CA与平面BCDE所成的角.
因为![]() 平面ADE,所以
平面ADE,所以![]() ,
,
在直角梯形BCDE中,作![]() 于
于![]() ,则四边形
,则四边形![]() 为矩形,
为矩形,![]()
则![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
在直角三角形ACD中,![]() ,
,
又![]() ,
,
在![]() 中,
中,![]()
所以![]()
所以![]() ,
,
所以![]() ,
,
所以直线CA与平面BCDE所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,∠ABD=60°,现将长方形ABCD沿着对角线BD折起,使平面ABD⊥平面BCD,则折后几何图形的外接球表面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行的“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如下表,该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中一等奖代表队有6人.
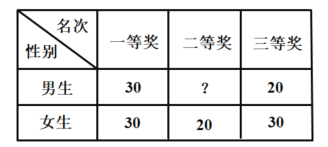
(1)求二等奖代表队的男生人数;
(2)从前排就坐的三等奖代表队员5人(2男3女)中随机抽取3人上台领奖,请求出只有一个男生上台领奖的概率;
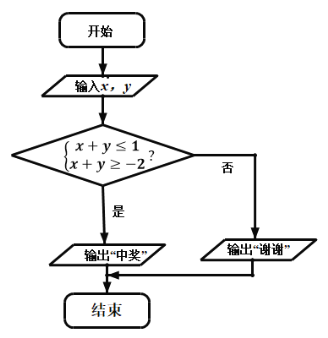
(3)抽奖活动中,代表队员通过操作按键,使电脑自动产生[![]() 2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2,△ADC沿AC折起,使得平面ADC⊥平面ABC,E为AB的中点,连接DE,DB(如图2).
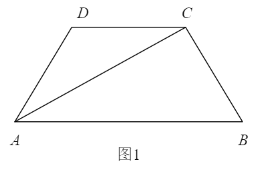
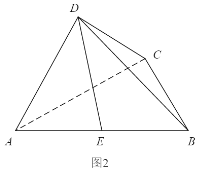
(1)求证:BC⊥AD
(2)求直线DE与平面BCD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受突如其来的新冠疫情的影响,全国各地学校都推迟2020年的春季开学.某学校“停课不停学”,利用云课平台提供免费线上课程.该学校为了解学生对线上课程的满意程度,随机抽取了500名学生对该线上课程评分.其频率分布直方图如下:若根据频率分布直方图得到的评分低于80分的概率估计值为0.45.
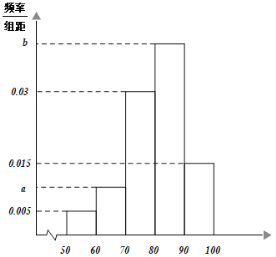
(1)(i)求直方图中的a,b值;
(ii)若评分的平均值和众数均不低于80分视为满意,判断该校学生对线上课程是否满意?并说明理由(同一组中的数据用该组区间的中点值为代表);
(2)若采用分层抽样的方法,从样本评分在[60,70)和[90,100]内的学生中共抽取5人进行测试来检验他们的网课学习效果,再从中选取2人进行跟踪分析,求这2人中至少一人评分在[60,70)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“珠算之父”程大位是我国明代著名的数学家,他的应用巨著《算法统综》中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节四升五,上梢四节三升八,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节竹的容积为
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PAPD,E,F分别为AD,PB的中点.求证:
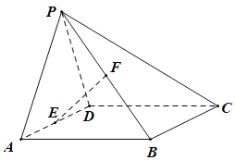
(1)EF//平面PCD;
(2)平面PAB平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司A产品生产的投入成本x(单位:万元)与产品销售收入y(单位:十万元)存在较好的线性关系,下表记录了该公司最近8次该产品的相关数据,且根据这8组数据计算得到y关于x的线性回归方程为![]() .
.
x(万元) | 6 | 7 | 8 | 11 | 12 | 14 | 17 | 21 |
y(十万元) | 1.2 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.9 |
(1)求![]() 的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
(2)该公司B产品生产的投入成本u(单位:万元)与产品销售收入v(单位:十万元)也存在较好的线性关系,且v关于u的线性回归方程为![]() .
.
(i)估计该公司B产品投入成本30万元后的毛利率(毛利率![]() );
);
(ii)判断该公司A,B两个产品都投入成本30万元后,哪个产品的毛利率更大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com