分析:(1)根据题意,作出
角的终边交单位圆于点P,再PM⊥x轴于M,过A(1,0)垂直于x轴的直线交OP的反向延长线于T.由三角函数线的定义,可得有向线段MP、OM、AT分别为
角的正弦线、余弦线、正切线;
(2)用类似(1)的方法作图,可得图(2)中的有向线段M'P'、OM'、A'T'分别为-
角的正弦线、余弦线、正切线.
解答:解:(1)∵
∈(
,π)
∴作出
角的终边如图所示,交单位圆于点P
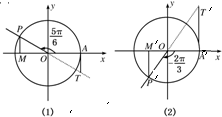
作PM⊥x轴于M,则有向线段MP=sin
,有向线段OM=cos
设过A(1,0)垂直于x轴的直线交OP的反向延长线于T,
则有向线段AT=tan
综上所述,图(1)中的有向线段MP、OM、AT分别为
角的正弦线、余弦线、正切线;
(2)∵-
∈(-π,-
)
∴在第三象限内作出-
角的终边如图所示,交单位圆于点P'
用类似(1)的方法作图,可得图(2)中的有向线段M'P'、OM'、A'T'分别为-
角的正弦线、余弦线、正切线.
点评:本题给出两个角,要求作出它们的正弦线、余弦线、正切线.着重考查了三角函数的定义、三角函数线的作法等知识,属于基础题.



