
分析 (1)求出A中不等式的解集确定出A,把m=2代入B中不等式求出解集确定出B,找出两集合的交集即可;
(2)表示出B中不等式的解集,由A与B的交集为B,得到B为A的子集,分B为空集与B不为空集两种情况求出m的范围即可.
解答 解:(1)由A中不等式变形得:log2(x+2)<2=log24,即0<x+2<4,
解得:-2<x<2,即A=(-2,2),
把m=2代入B中不等式得:(x+1)(x-3)<0,
解得:-1<x<3,即B=(-1,3),
则A∩B=(-1,2);
(2)由题意得:A=(-2,2),B=(1-m,1+m),且A∩B=B,
当B=∅,即1-m≥1+m时,解得:m≤0,满足题意;
当B≠∅,即1-m<1+m,解得:m>0,则有$\left\{\begin{array}{l}{1-m≥-2}\\{1+m≤2}\end{array}\right.$,
解得:0<m≤1,
综上,m的范围是m≤1.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
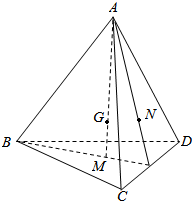 如图,已知M、N分别为四面体ABCD的面BCD与面ACD的重心,且G为AM上一点,且GM:GA=1:3,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BG}$,$\overrightarrow{BN}$.
如图,已知M、N分别为四面体ABCD的面BCD与面ACD的重心,且G为AM上一点,且GM:GA=1:3,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BG}$,$\overrightarrow{BN}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°.则以下结论中正确的有(1)(2)(4).
如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°.则以下结论中正确的有(1)(2)(4).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com